题目内容
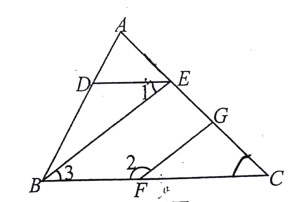
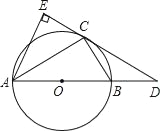
【题目】如图1,将一张矩形纸ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
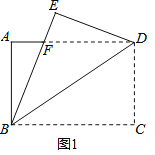
(1)求证:![]() 是等腰三角形;
是等腰三角形;
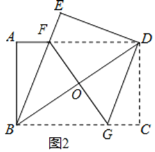
(2)如图2,过点D作![]() ,交BC于点G,连接FG交BD于点O.
,交BC于点G,连接FG交BD于点O.
①试判断四边形BGDF的形状,并说明理由;
②若![]() ,
,![]() ,求FG的长.
,求FG的长.
【答案】(1)详见解析;(2)四边形BGDF为菱形;(3)![]() ,
,
【解析】
(1)根据两直线平行内错角相等及折叠特性判断;
(2)①根据已知矩形性质及第一问证得邻边相等判断;
②根据折叠特性设未知边,构造勾股定理列方程求解.
(1)证明:如图1,根据折叠,∠DBC=∠DBE,
又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF
∴![]() 是等腰三角形;
是等腰三角形;
(2)①∵四边形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵DG∥BE,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=3,AD=4,
∴BD=5.
∴OB=![]() BD=
BD=![]() .
.
假设DF=BF=x,∴AF=AD-DF=4-x.
∴在直角△ABF中,AB2+AF2=BF2,即32+(4-x)2=x2,
解得x=![]() ,
,
即BF=![]() ,
,
∴FO=![]() ,
,
∴FG=2FO=![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目