题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() .
.
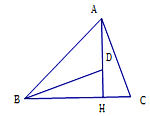
(1)求证:![]()
(2)如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别对应点
分别对应点![]() ),设射线
),设射线![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间满足的数量关系,并说明理由.
之间满足的数量关系,并说明理由.
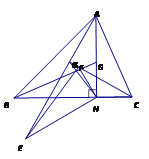
【答案】(1)证明见解析(2)EF=2HG
【解析】分析:(1)先判断出AH=BH,再判断出△BHD≌△AHC即可求解.(2)方法一、先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可;方法二、取EF的中点K,连接GK,HK,先证明GK=HK=
,然后判断出△AQC∽△GQH,用相似比即可;方法二、取EF的中点K,连接GK,HK,先证明GK=HK=![]() EF,再证明△GKH是等边三角形即可.
EF,再证明△GKH是等边三角形即可.
详解:(1)在Rt△AHB中,∠ABC=45°,
∴AH=BH,
在△BHD和△AHC中,
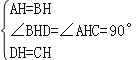 ,
,
∴△BHD≌△AHC,
∴![]()
(2)方法1:如图1,
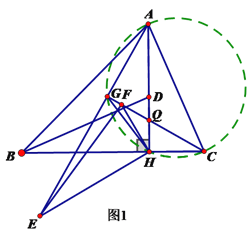
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQH,
∴△AQC∽△GQH,
∴![]() ,
,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴EF=BD,
由(1)知,BD=AC,
∴EF=AC
∴![]()
即:EF=2HG.
方法2:如图2,取EF的中点K,连接GK,HK,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
由旋转知,∠EHF=90°,
∴EK=HK=![]() EF
EF
∴EK=GK=![]() EF,
EF,
∴HK=GK,
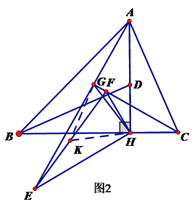
∵EK=HK,
∴∠FKG=2∠AEF,
∵EK=GK,
∴∠HKF=2∠HEF,
由旋转知,∠AHF=30°,
∴∠AHE=120°,
由(1)知,BH=AH,
∵BH=EH,
∴AH=EH,
∴∠AEH=30°,
∴∠HKG=∠FKG+∠HKF=2∠AEF+2∠HEF=2∠AEH=60°,
∴△HKG是等边三角形,
∴GH=GK,
∴EF=2GK=2GH,
即:EF=2GH.