题目内容
观察下列等式：
=1-
，
=
-
，
=
-
，将以上三个等式相加得：
+
+
=1-
+
-
+
-
=1-
=
．
（1）猜想并写出：
=______．
（2）直接写出结果：
+
+
+…+
=______．
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
（1）猜想并写出：
| 1 |
| n(n+1) |
（2）直接写出结果：
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
（1）根据题中的一系列等式，可得
=
-
；
（2）
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
．
故答案为：（1）
-
；（2）
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
（2）
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2006 |
| 1 |
| 2007 |
| 1 |
| 2007 |
| 2006 |
| 2007 |
故答案为：（1）
| 1 |
| n |
| 1 |
| n+1 |
| 2006 |
| 2007 |
练习册系列答案
开心蛙口算题卡系列答案
相关题目
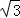）2﹣|﹣2|= ．