Question

【题目】已知：在△ABC中，AC=a，AB与BC所在直线成45°角，AC与BC所在直线形成的夹角的余弦值为（即cosC=），则AC边上的中线长是_____________．

Answer 1

【答案】或

【解析】

解：分两种情况：

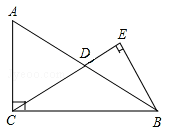
①△ABC为锐角三角形时，如图1．

作△ABC的高AD，BE为AC边的中线．

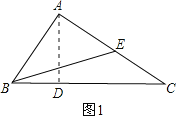
∵在直角△ACD中，AC=a，cosC=，

∴CD=a，AD=a．

∵在直角△ABD中，∠ABD=45°，

∴BD=AD=a，

∴BC=BD+CD=a．

在△BCE中，由余弦定理，得

BE2=BC2+EC2-2BCECcosC

∴BE=；

②△ABC为钝角三角形时，如图2．

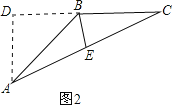
作△ABC的高AD，BE为AC边的中线．

∵在直角△ACD中，AC=a，cosC=，

∴CD=a，AD=a．

∵在直角△ABD中，∠ABD=45°，

∴BD=AD=a，

∴BC=BD+CD=a．

在△BCE中，由余弦定理，得

BE2=BC2+EC2-2BCECcosC

∴BE=．

综上可知AC边上的中线长是或．