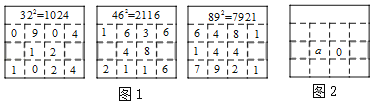题目内容
【题目】问题背景:
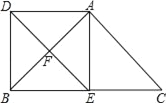
如图1,△ABC为等边三角形,作AD⊥BC于点D,将∠ABC绕点B顺时针旋转30°后,BA,BC边与射线AD分别交于点E,F,求证:△BEF为等边三角形.
迁移应用:
如图2,△ABC为等边三角形,点P是△ABC外一点,∠BPC=60°,将∠BPC绕点P逆时针旋转60°后,PC边恰好经过点A,探究PA,PB,PC之间存在的数量关系,并证明你的结论;
拓展延伸:
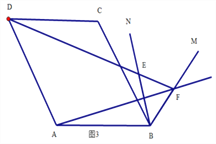
如图3,在菱形ABCD中,∠ABC=60°,将∠ABC绕点B顺时针旋转到如图所在的位置得到∠MBN,F是BM上一点,连接AF,DF,DF交BN于点E,若B,E两点恰好关于直线AF对称.
(1)证明△BEF是等边三角形;
(2)若DE=6,BE=2,求AF的长.


【答案】(1)见解析;(2) PC=PA+PB;(3)![]()
【解析】分析: (1)根据等边三角形的性质得到∠EBF=60°, 又由BD⊥AC得到∠BED=60°,从而得出结论; (2)在PC上截取PD=PB,连接BD,通过证明△APB≌△CBG得PA=GC,即可得出结论;(3) ①依据B,E两点关于直线AF对称得FE=FB,又由于∠EBF=60°即可得出结论; ②连接AE,过点A作AH⊥DE于点H,可得DH=3,HF=5, ∠EFA=30°,在Rt△AHF中,利用∠HFA的余弦即可求出AF的值.
详解:
(1)证明:∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°,
由题意得,∠ABE=30°,∠EBF=60°,
∴∠EBD=∠FBD=30°,
∵BD⊥AC,∴∠BED=60°,
∴△BEF为等边三角形;
(2) PC=PA+PB.
证明:在PC上截取PD=PB,连接BD,

∵∠BPC=60°,∴△BPG为等边三角形,
∴BG=BP,∠PBG=60°,PB=BG,
∴∠PBA+∠ABG=∠ABG+∠GBC=60°
∴∠PBA=∠GBC
又AB=BC,∴△APB≌△CBG,
∴PA=GC,
∴PC=PG+CG=PB+PA
(3)①∵B,E两点关于直线AF对称,∴FE=FB,
∵∠EBF=60°,∴△BEF是等边三角形;
②连接AE,过点A作AH⊥DE于点H,
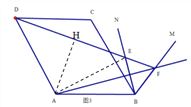
∵B,E两点关于直线AF对称,∴AE=AB,
∵四边形ABCD是菱形,∴AB=AD,
∴AE=AD,所以DH=HE=![]() DE=3,
DE=3,
∴HF=HE+EF=3+2=5,
由①知,△BEF是等边三角形,FA⊥EB,
∴∠EFA=![]() ∠EFB=30°
∠EFB=30°
.在Rt△AHF中,cos∠HFA=![]() =
=![]() ,
,
∴AF=![]() .
.
点睛:本题考查了等边三角形的性质,全等三角形的判定与性质以及三角函数, 解题的关键是正确作出辅助线,灵活运用三角形相似.