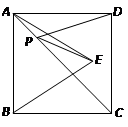题目内容
如图①在梯形ABCD中,AD∥BC。AB=DC
(1)如果点P,E和F分别是BC,AC和BD的中点,证明:AB=PE+PF
(2)如果点P是线段BC上任意一点(中点除外),PE∥AB,PF∥DC,如图②所示,那么AB=PE+PF这个结论还成立吗?请说明理由
(3)如果点P在线段BC的延长线上, PE∥AB,PF∥DC,其他条件不变,那么结论AB=PE+PF是否成立?直接写出结论,不必证明。
(1)如果点P,E和F分别是BC,AC和BD的中点,证明:AB=PE+PF
(2)如果点P是线段BC上任意一点(中点除外),PE∥AB,PF∥DC,如图②所示,那么AB=PE+PF这个结论还成立吗?请说明理由
(3)如果点P在线段BC的延长线上, PE∥AB,PF∥DC,其他条件不变,那么结论AB=PE+PF是否成立?直接写出结论,不必证明。

(1)证明:∵P、F分别为BC、BD的中点,
∴PF=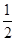 CD,
CD,
同理:PE=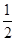 AB,
AB,
又∵AB=CD,
∴PF=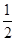 AB,
AB,
∴AB=PE+PF;
(2)答:成立,AB=PE+PF.
证明:延长PE交AD于G,
∵AG∥BP,AB∥PG,
∴四边形ABPG为平行四边形.
∴AG=BP,∠AGP=∠ABP.
∵四边形ABCD是等腰梯形,
∴AB=DC,
∴∠ABC=∠DCB且BC为公共边,
∴△ABC≌△DCB(SAS),
∴∠ACB=∠FBP,
又∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠FBP,
∵FP∥CD,
∴∠FPB=∠DCB.
∴∠FPB=∠AGE.
∴△AEG≌△BPF(ASA).
∴AB=PG=PE+PF.
(3)答:AB=PF-PE.
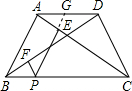
∴PF=
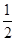 CD,
CD,同理:PE=
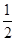 AB,
AB,又∵AB=CD,
∴PF=
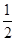 AB,
AB,∴AB=PE+PF;
(2)答:成立,AB=PE+PF.
证明:延长PE交AD于G,
∵AG∥BP,AB∥PG,
∴四边形ABPG为平行四边形.
∴AG=BP,∠AGP=∠ABP.
∵四边形ABCD是等腰梯形,
∴AB=DC,
∴∠ABC=∠DCB且BC为公共边,
∴△ABC≌△DCB(SAS),
∴∠ACB=∠FBP,
又∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠FBP,
∵FP∥CD,
∴∠FPB=∠DCB.
∴∠FPB=∠AGE.
∴△AEG≌△BPF(ASA).
∴AB=PG=PE+PF.
(3)答:AB=PF-PE.

(1)由于PF是△BDC的中位线,PE是△ABC的中位线而AB=CD,故有PF=PE;
(2)延长PE交AD于G,易证:四边形ABPG为平行四边形,可证:△AEG≌△BPF,得EG=PF,故有AB=PG=PE+PF;
(3)延长AD交EP于G,易证:四边形DGPC为平行四边形,可证:△DFG≌△CPF,得FG=PF,故有AB=PG=PE-PF.
(2)延长PE交AD于G,易证:四边形ABPG为平行四边形,可证:△AEG≌△BPF,得EG=PF,故有AB=PG=PE+PF;
(3)延长AD交EP于G,易证:四边形DGPC为平行四边形,可证:△DFG≌△CPF,得FG=PF,故有AB=PG=PE-PF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 的面积为12,
的面积为12, 是等边三角形,点
是等边三角形,点 在正方形
在正方形 上有一点
上有一点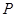 , 使
, 使 的和最小,则这个最小值为( )
的和最小,则这个最小值为( )