题目内容
如图所示,正方形 的面积为12,
的面积为12, 是等边三角形,点
是等边三角形,点 在正方形
在正方形 内,在对角线
内,在对角线 上有一点
上有一点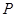 , 使
, 使 的和最小,则这个最小值为( )
的和最小,则这个最小值为( )
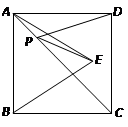

 的面积为12,
的面积为12, 是等边三角形,点
是等边三角形,点 在正方形
在正方形 内,在对角线
内,在对角线 上有一点
上有一点 , 使
, 使 的和最小,则这个最小值为( )
的和最小,则这个最小值为( )

A. | B. | C.3 | D.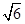 |
A
解:设BE与AC交于点F(P'),连接BD,
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
即P在AC与BE的交点上时,PD+PE最小,为BE的长度;
∵正方形ABCD的面积为12,
∴AB=2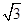 .
.
又∵△ABE是等边三角形,
∴BE=AB=2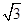 .
.
故所求最小值为2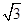 .
.
故答案为A
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
即P在AC与BE的交点上时,PD+PE最小,为BE的长度;
∵正方形ABCD的面积为12,
∴AB=2
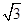 .
.又∵△ABE是等边三角形,
∴BE=AB=2
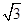 .
.故所求最小值为2
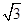 .
.故答案为A

练习册系列答案
相关题目

 ABCD中,已知点A(﹣1,0),B(2,0),D(0,1).则点C的坐标为 .
ABCD中,已知点A(﹣1,0),B(2,0),D(0,1).则点C的坐标为 . 边长为4,
边长为4, 分别是
分别是 上的两个动点,当
上的两个动点,当 点在
点在 上运动时,保持
上运动时,保持 和
和 垂直,设
垂直,设 ,梯形
,梯形 的面积为
的面积为 ,下列结论
,下列结论

 ∽
∽
 的函数关系式为:
的函数关系式为:


 。
。 ①②③
①②③  ①③④
①③④  ②③④
②③④  ②④
②④



