题目内容
【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

【答案】18m
【解析】分析:如图作EF⊥AB于F,则四边形EFBD是矩形.设EF=AF=x米.在Rt△PAB中,AB=x+3,PB=30+x,根据tan22°=![]() ,可得
,可得![]() =
=![]() ,解方程即可解决问题.
,解方程即可解决问题.
详解:如图,作EF⊥AB于F,则四边形EFBD是矩形.
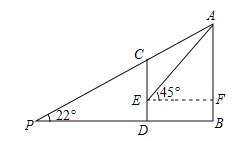
∵∠AEF=45°,∠AFE=90°,∴∠AEF=∠EAF=45°,∴EF=AF,设EF=AF=x,则BD=EF=x.在Rt△PAB中,∵AB=x+3,PB=30+x,∴tan22°=![]() =
=![]() ,解得:x=15,∴AB=x+3=18.
,解得:x=15,∴AB=x+3=18.
答:教学楼AB的高度约为18m.

练习册系列答案
相关题目
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.