Ő‚ńŅńŕ»›
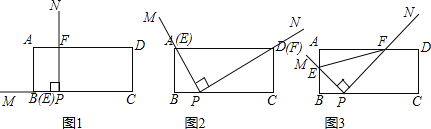
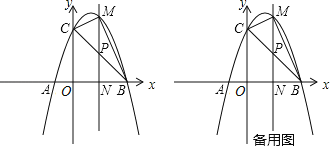
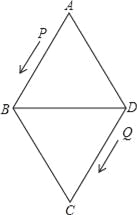
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ń‚–őABCDĶńĪŖ≥§ő™24ņŚ√◊£¨°ŌA=60°„£¨Ķ„Pī”Ķ„A≥Ų∑Ę—ōŌŖ¬∑AB°ķBD◊ų‘»ňŔ‘ň∂Į£¨Ķ„Qī”Ķ„DÕ¨ Ī≥Ų∑Ę—ōŌŖ¬∑DC°ķCB°ķBA◊ų‘»ňŔ‘ň∂Į£ģ
£®1£©«ůBDĶń≥§£Ľ
£®2£©“—÷™Ķ„P°ĘQ‘ň∂ĮĶńňŔ∂»∑÷Īūő™4ņŚ√◊/√Ž£¨5ņŚ√◊/√Ž£¨ĺ≠Ļż12√Žļů£¨P°ĘQ∑÷ĪūĶĹīÔM°ĘNŃĹĶ„£¨»ŰįīĹ«Ķńīů–°ĹÝ––∑÷ņŗ£¨«Žń„»∑∂®°ųAMN «ńń“Ľņŗ»żĹ«–ő£¨≤ĘňĶ√ųņŪ”…£Ľ
£®3£©…Ť£®2£©÷–ĶńĶ„P°ĘQ∑÷Īūī”M°ĘNÕ¨ Ī—ō‘≠¬∑∑ĶĽō£¨Ķ„PĶńňŔ∂»≤ĽĪš£¨Ķ„QĶńňŔ∂»łńĪšő™aņŚ√◊/√Ž£¨ĺ≠Ļż3√Žļů£¨P°ĘQ∑÷ĪūĶĹīÔE°ĘFŃĹĶ„£¨»Ű°ųBEF”Ž£®2£©÷–Ķń°ųAMNŌŗň∆£¨ ‘«ůaĶń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©BD=24£®2£©°ųAMN «÷ĪĹ«»żĹ«–ő£®3£©2ĽÚ6ĽÚ12
°ĺĹ‚őŲ°Ņ
‘Ő‚£®1£©łýĺ›Ń‚–őĶń–‘÷ ÷§°ųABD «Ķ»ĪŖ»żĹ«–őľīŅ…£Ľ
£®2£©«ů≥ŲP Q◊ŖĶńĺŗņŽ£¨‘Ŕłýĺ›Ķ»—Ł»żĹ«–ő–‘÷ ľīŅ…Õ∆≥Ųīūįł£Ľ
£®3£©∑÷ő™»ż÷÷«ťŅŲ£ļłýĺ›Ōŗň∆£¨Ķ√ĶĹĪ»ņż Ĺ£¨«ů≥ŲQ◊ŖĶńĺŗņŽ£¨ľīŅ…«ů≥Ųīūįł£ģ
‘Ő‚Ĺ‚őŲ£ļ£®1£©°ŖŃ‚–őABCD£¨
°ŗAB=AD£¨
°Ŗ°ŌA=60°„£¨
°ŗ°ųABD «Ķ»ĪŖ»żĹ«–ő£¨
°ŗBD=AB=24ņŚ√◊£ģ
īū£ļBD=24ņŚ√◊£ģ
£®2£©12√Ž Ī£¨P◊ŖŃň4°Ń12=48£¨
°ŖAB+BD=24+24=48£¨
°ŗPĶĹDĶ„£¨
Õ¨ņŪQĶĹABĶń÷–Ķ„…Ō£¨
°ŖAD=BD£¨
°ŗMN°ÕAB£¨
°ŗ°ųAMN «÷ĪĹ«»żĹ«–ő£ģ
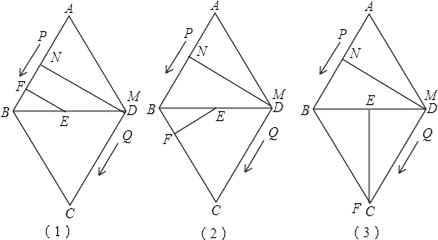
£®3£©”–»ż÷÷«ťŅŲ£ļ»ÁÕľ£®2£©
°ŌANM=°ŌEFB=90°„£¨°ŌA=°ŌDBF=60°„£¨DE=3°Ń4=12=![]() AD£¨
AD£¨
łýĺ›Ōŗň∆»żĹ«–ő–‘÷ Ķ√£ļBF=![]() AN=6£¨
AN=6£¨
°ŗNB+BF=12+6=18£¨
°ŗa=18°¬3=6£¨
Õ¨ņŪ£ļ»ÁÕľ£®1£©«ů≥Ųa=2£Ľ
»ÁÕľ£®3£©a=12£ģ
°ŗaĶń÷Ķ «2ĽÚ6ĽÚ12£ģ

 ņľÕįŔÕ®∆ŕń©ĹūĺŪŌĶŃ–īūįł
ņľÕįŔÕ®∆ŕń©ĹūĺŪŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņń≥◊®¬ŰĶÍ◊ľĪłĻļĹÝľ◊°Ę““ŃĹ÷÷‘ň∂Į–¨£¨∆šĹÝľŘļÕ ŘľŘ»ÁŌ¬ĪŪňý ĺ°£“—÷™”√3000‘™ĻļĹÝľ◊÷÷‘ň∂Į–¨Ķń żŃŅ”Ž”√2400‘™ĻļĹÝ““÷÷‘ň∂Į–¨Ķń żŃŅŌŗÕ¨.
‘ň∂Į–¨ľŘłŮ | ľ◊ | ““ |
Ĺݾؑ™/ňę) | m | m-30 |
ŘľŘ(‘™/ňę) | 300 | 200 |
(1)«ůmĶń÷Ķ£Ľ
(2)“™ ĻĻļĹÝĶńľ◊£¨““ŃĹ÷÷‘ň∂Į–¨Ļ≤200ňęĶń◊‹ņŻ»ů≤Ľ…Ŕ”ŕ21700‘™«“≤Ľ≥¨Ļż22300‘™£¨ő ł√◊®¬ŰĶÍ”–ľł÷÷ĹÝĽű∑Ĺįł?
(3)‘ŕ(2)ĶńŐűľĢŌ¬£¨◊®¬ŰĶÍĺŲ∂®∂‘ľ◊÷÷‘ň∂Į–¨√Ņňę”ŇĽ›a(60<a<80)‘™≥Ų Ř£¨““÷÷‘ň∂Į–¨ľŘłŮ≤ĽĪš£¨ń«√īł√◊®¬ŰĶÍ“™ĽŮĶ√◊ÓīůņŻ»ů”¶»ÁļőĹÝĽű?