题目内容
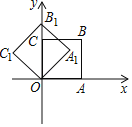
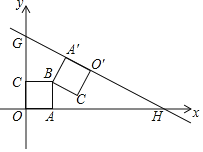
【题目】如图,直线y=![]() x+b(b>2)与x轴,y轴分别交于H,G两点,边长为2的正方形OABC的边OA,OC分别在x轴,y轴上,点B在第一象限,正方形OABC绕点B逆时针旋转,OA的对应边O'A'恰好落在直线GH上,则b的值为( )
x+b(b>2)与x轴,y轴分别交于H,G两点,边长为2的正方形OABC的边OA,OC分别在x轴,y轴上,点B在第一象限,正方形OABC绕点B逆时针旋转,OA的对应边O'A'恰好落在直线GH上,则b的值为( )
A.4![]() B.
B.![]() C.5D.6
C.5D.6
【答案】C
【解析】
过点A′作A′M⊥x轴,交CB的延长线与M,交x轴于D;可以证明∠BA′M=∠H,在Rt△A′BM中,A′B=2,tan∠BA′M=![]() ,分别求出BM=
,分别求出BM=![]() ,A′M=
,A′M=![]() ,确定A′的坐标为A′(
,确定A′的坐标为A′(![]() ,
,![]() ),再将点A′(
),再将点A′(![]() ,
,![]() )代入y=
)代入y=![]() x+b,即可求解.
x+b,即可求解.![]()
解:过点A′作A′M⊥x轴,交CB的延长线与M,交x轴于D,
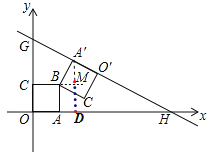
∵∠BA′M+∠MA′O′=90°,∠H+∠HA′M=90°,
∴∠BA′M=∠OHG,
∵y=![]() x+b,
x+b,
∴tan∠BA′M=tan∠OHG=![]() ,
,
设BM=5m,A′M=12m,
∵A′B=2,
∴(5m)2+(12m)2=4,
∴m=![]() ,
,
∴BM=![]() ,A′M=
,A′M=![]() ,
,
∵B(2,2),
∴A′(![]() ,
,![]() ),
),
将点A′(![]() ,
,![]() )代入y=
)代入y=![]() x+b,得
x+b,得
![]() ×
×![]() +b=
+b=![]() ,
,
∴b=5;
故选:C.

练习册系列答案
相关题目