��Ŀ����
����Ŀ���ڲ���ڼ䣬ij���̶����˼��ֲ�Ҷ90�֣����ֲ�Ҷ80�֣�����A��B�����ͺŵĻ�����20��������أ���֪A�ͻ���ÿ���˷�Ϊ0.4��Ԫ��B�ͻ���ÿ���˷�Ϊ0.6��Ԫ����13�֣�
��1����A�ͻ�������x�������˷�Ϊy��Ԫ��д��y��x�ĺ�����ϵʽ��
��2����һ��A�ͻ�����װ���ֲ�Ҷ6�֣����ֲ�Ҷ2�֣�һ��B�ͻ�����װ���ֲ�Ҷ3�֣����ֲ�Ҷ7�֣�����Ҫ����A��B�����ͺŻ���һ��������������Ҷ�������ļ������䷽����
��3��˵�����ַ����˷����٣������˷��Ƕ�����Ԫ��
���𰸡���1��y=��0.2x+12��(2) �������䷽������A�ͻ���10����B�ͻ���10������A�ͻ���11����B�ͻ���9����
��A�ͻ���12����B�ͻ���8����(3) �������˷����٣������˷�Ϊ9.6��Ԫ��
�������������������1����A�ֻ���Ϊx������B�ֻ���Ϊ��20-x���������ʾ�����ֳ��ķ��õĺ;����ܷ��ã��ݴ˼�����⣻
��2���ֿ��м��ֲ�Ҷ90�֣�A�ͻ�����װ���ֲ�Ҷ6�֣����ֲ�Ҷ2�֣�һ��B�ͻ�����װ���ֲ�Ҷ3�֣����ֲ�Ҷ7�֣��ݴ˼��ɵõ�һ������x�IJ���ʽ�飬�ٸ���x���������������x��ֵ���Ӷ�ȷ�����䷽����
��3���˷ѿ��Ա�ʾΪx�ĺ��������ݺ��������ʣ�������⣮
�����������1����A�ֻ���Ϊx������B�ֻ���Ϊ��20-x������
�������⣬��y=0.4x+0.6��20-x��=-0.2x+12��
��2���������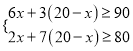 ��
��
���10��x��12��
�֡�xΪ��������
��x=10��11��12��
��20-x=10��9��8��
���������������䷽����
��A�ͻ���10����B�ͻ���10����
��A�ͻ���11����B�ͻ���9����
��A�ͻ���12����B�ͻ���8����
��3���߷������˷ѣ�10��0.4+10��0.6=10����Ԫ����
�������˷ѣ�11��0.4+9��0.6=9.8����Ԫ����
�������˷ѣ�12��0.4+8��0.6=9.6����Ԫ����
������˷����٣������˷�Ϊ9.6��Ԫ��

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�����Ŀ�����䷽���ⷽ��x2+8x+9=0�����κ�Ľ����ȷ���ǣ� ��
A.��x+4��2=��7
B.��x+4��2=��9
C.��x+4��2=7
D.��x+4��2=25
����Ŀ��ij���̶���14��Ա�������ǵĹ��ּ���Ӧÿ��ÿ�¹������±���ʾ��
���� | ���� | ÿ��ÿ�¹���/Ԫ |
�繤 | 5 | 7000 |
ľ�� | 4 | 6000 |
�߹� | 5 | 5000 |
�ָù��̶ӽ�������Ա����������ľ��2�������ӵ繤���߹���1���������ǰ��ȣ��ù��̶�Ա���¹��ʵķ��������С���������䡱�����