题目内容
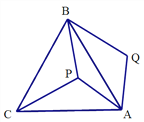
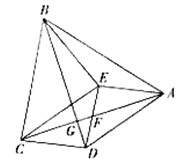
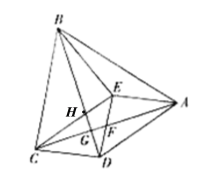
【题目】如图,四边形ABCD内一点E满足EB=EC,EA=ED,∠BEC=∠AED=90°,AC交DE于点F,交BD于点G.
(1)∠AGB的度数为
(2)若四边形AECD是平行四边形
①求证:AC=AB
②若AE=2,求AF·CG的值
【答案】(1)90°;(2)①见解析,②AFCG= 4.
【解析】
(1)先利用SAS证明△BED≌△CEA,得∠DBE=∠ACE,由∠BHE=∠CHG,得到∠HGC=∠BEH=90°,从而∠AGB=90°;
(2)①由(1)可知△BED≌△CEA,得BD=CA,由平行四边形AECD,得AE=CD=DE,∠AED=∠EDC=90°,从而∠CED=45°,∠BED=135°,利用周角得到∠BEA=135°,可证△BAE≌△BDE,得到BD=BA,从而AC=AB;
②由①可知,△CAE≌△BAE,得∠BAE=∠EAC=∠BDE,由∠EAC+∠AFE=90°,∠GFD=∠AFE,得∠GFD+∠BDE=90°,从而∠CGD=90°,可证△CGD∽△AEF,根据相似三角形的性质得到![]() =
=![]() ,由AE=4,从而得解.
,由AE=4,从而得解.
解:(1)∵∠BEC=∠AED=90°,
∴∠BED=∠CEA,
又∵BE=EC,EA=ED,
∴△BED≌△CEA,
∴∠DBE=∠ACE,
又∵∠BHE=∠CHG,
∴∠HGC=∠BEH=90°,
∴∠AGB=90°;
(2)①∵四边形AECD是平行四边形,
∴∠AED=∠EDC=90°,AE=CD,
∵△ADE是等腰直角三角形,
∴AE=ED,∴ED=CD,
∴∠CED=45°,
∴∠BED=90°+45°=135°,
∵∠AED=∠BEC=90°,
∴∠AEB=360°-90°-90°-45°=135°,又EB=EB,ED=EA,
∴△BAE≌△BDE(SAS),
∴DB=AB;
∵∠BEC=∠AED=90°,
∴∠BED=∠CEA,
∵EB=EC,EA=ED,
∴△BED≌△CEA,
∴BD=CA,
∴AC=AB.
②∵△BAE≌△BDE,
∴△CAE≌△BAE,
∴∠BAE=∠CAE=∠BDE,
∵∠EAF+∠AFE=90°,
∴∠AFE+∠BAE=90°,
∵∠GFD=∠AFE,∠EDB=∠EAB,
∴∠EDB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△AEF,
∴![]() =
=![]() ,
,
∴AFCG=CDAE=4.
故答案为(1)90°;(2)①见解析,②4.