题目内容
【题目】如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )

A、3或4![]() B、4或3
B、4或3![]() C、3或4 D、3
C、3或4 D、3![]() 或4
或4![]()
【答案】D.
【解析】
试题分析:如图,过点A′作A′M⊥BC于点M.设CM=A′M=x,则BM=7-x.在直角△A′MB中,由勾股定理得到:A′M2=A′B2-BM2=25-(7-x)2.由此求得x的值;然后在等腰Rt△A′CM中,CA′=2A′M.
试题解析:如图所示,过点A′作A′M⊥BC于点M.

如图所示,过点A′作A′M⊥BC于点M.
∵点A的对应点A′恰落在∠BCD的平分线上,
∴设CM=A′M=x,则BM=7-x,
又由折叠的性质知AB=A′B=5,
∴在直角△A′MB中,由勾股定理得到:A′M2=A′B2-BM2=25-(7-x)2,
∴25-(7-x)2=x2,
∴x=3或x=4,
∵在等腰Rt△A′CM中,CA′=2A′M,
∴CA′=3![]() 或4
或4![]() .
.
故选D.

练习册系列答案
相关题目
【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图. 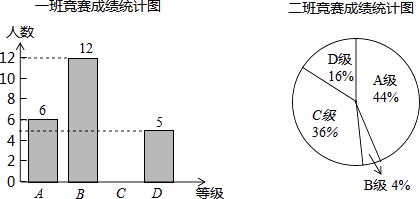
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(1)把一班竞赛成绩统计图补充完整;
(2)写出表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(3)请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.