Question

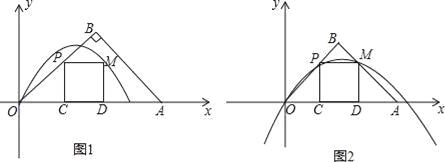
【题目】如图1在平面直角坐标系中．等腰Rt△OAB的斜边OA在x轴上．P为线段OB上﹣动点（不与O，B重合）．过P点向x轴作垂线．垂足为C．以PC为边在PC的右侧作正方形PCDM．OP=t，OA=3．设过O，M两点的抛物线为y=ax2+bx．其顶点N（m，n）

（1）写出t的取值范围　　，写出M的坐标：（　　，　　）；

（2）用含a，t的代数式表示b；

（3）当抛物线开向下，且点M恰好运动到AB边上时（如图2）

①求t的值；

②若N在△OAB的内部及边上，试求a及m的取值范围．

Answer 1

【答案】（1）0＜t＜，M（2t，t）；（2）b=；（3）①t=1；②≤m≤2．

【解析】试题分析：

试题解析：(1)如图1，∵△OAB为等腰直角三角形，OA=3，

∵P为线段OB上动点(不与O,B重合)，

∵四边形PCDM为正方形，

∴△POC为等腰直角三角形，

∴PC=OC=t，

∴OD=t+t=2t，

∴M(2t,t)；

(2)把M(2t,t)代入到中得：

1=4at+2b，

(3)①如图2,

∵

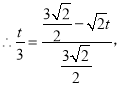
∴t=1；

②由(2)得： 即4a=12b，

顶点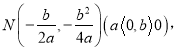

i)当时,即时，

解得

ii)当时,即

则

综上所述：a的取值为：

得：

∴