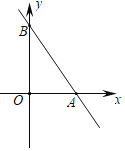题目内容
【题目】快车从M地出发沿一条公路匀速前往N地，慢车从N地出发沿同一条公路匀速前往M地，已知快车比慢车晚出发0.5小时，快车先到达目的地．设慢车行驶的时间为t（h），快慢车辆车之间的距离为s（km），s与t的函数关系如图1所示．
（1）求图1中线段BC的函数表达式；
（2）点D的坐标为 ，并解释它的实际意义；
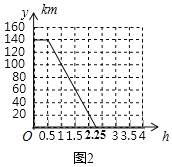
（3）设快车与N地的距离为y（km），请在图2中画出y关于慢车行驶时间t的函数图象．（标明相关数据）
【答案】（1）y＝﹣120x+180；（2）（
，90），慢车行驶了小时后，两车相距90千米；（3）详见解析．
【解析】
（1）由待定系数法可求解；
（2）先求出两车的速度和，即可求解；
（3）根据函数图象求出快车的速度，从而得y关于慢车行驶时间t的函数解析式，进而即可画出图象．
（1）设线段BC所在直线的函数表达式为：y＝kx+b（k，b为常数，k≠0）
∴
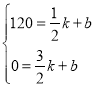，解得：
，
∴线段BC所在直线的函数表达式为：y＝﹣120x+180；
（2）由图象可得：两车的速度和＝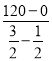
＝120（千米/小时），
∴120×（
）＝90（千米），
∴点D(
，90)，表示慢车行驶了小时后，两车相距90千米；
（3）由函数图象可知：快车从M地到N地花了
小时，慢车从N地到M地花了
小时，
∴快车与慢车的速度比=：
=2：1，
∴快车的速度为：120×
=80（千米/小时），M，N之间距离为：80×=140（千米），
∴y关于慢车行驶时间t的函数解析式为：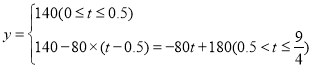
，
图象如图所示：
练习册系列答案
相关题目
