题目内容
【题目】如图，在平面直角坐标系xOy中，直线y＝﹣
x+4与x轴、y轴分别交于点A、B，M是y轴上的点（不与点B重合），若将△ABM沿直线AM翻折，点B恰好落在x轴正半轴上，则点M的坐标为（ ）
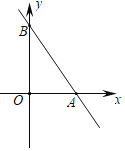
A.（0，﹣4 ）B.（0，﹣5 ）C.（0，﹣6 ）D.（0，﹣7 ）
【答案】C
【解析】
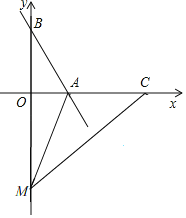
设沿直线AM将△ABM折叠，点B正好落在x轴上的C点，则有AB＝AC，而AB的长度根据已知可以求出，所以C点的坐标由此求出；又由于折叠得到CM＝BM，在直角△CMO中根据勾股定理可以求出OM，也就求出M的坐标．
设沿直线AM将△ABM折叠，点B正好落在x轴上的C点，
∵直线y＝﹣
x+4与x轴、y轴分别交于点A、B，
∴A（3，0），B（0，4），
∴AB＝
＝5，
设OM＝m，
由折叠知，AC＝AB＝5，CM＝BM＝OB+OM＝4+m，
∴OC＝8，CM＝4+m，
根据勾股定理得，64+m2＝（4+m）2，解得：m＝6，
∴M（0，﹣6），
故选：C．
练习册系列答案
相关题目
【题目】在一次数学测试中，同年级人数相同的甲、乙两个班的成绩统计如下表：
班级 | 平均分 | 中位数 | 方差 |
甲班 |
|
|
|
乙班 |
|
|
|
数学老师让同学们针对统计的结果进行一下评估，学生的评估结果如下：
这次数学测试成绩中，甲、乙两个班的平均水平相同；
甲班学生中数学成绩95分及以上的人数少；
乙班学生的数学成绩比较整齐，分化较小．
上述评估中，正确的是______
填序号
