题目内容
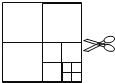
【题目】如图所示,有若干边长为1的正方形卡片,第1次并排摆2张黑色卡片,铺成一个长方形;第2次在黑色卡片上方和右侧摆白色卡片,所有卡片铺成了一个较大的长方形;第3次继续在白色卡片上方和右侧摆黑色卡片,所有卡片铺成了一个更大的长方形;以此类推,请解决以下问题:
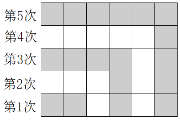
(1)仅第10次要用去______张卡片,摆完第10次后,总共用去_______张卡片.
(2)你知道 2+4+6+8+……+2n的结果是多少吗?写出结果,结合图形规律说明你的理由.
(3)求出从第51次至第100次所摆卡片的数量之和.
【答案】(1)20,110;(2)2+4+6+8+……+2n= n(n+1);(3)从第51次至第100次所摆卡片的数量之和7550.
【解析】
(1)观察图形可知:第1次共用去卡片2张,可以看成水平方向1张,竖直方向1张;第2次共用去卡片4张,可以看成水平方向2张,竖直方向2张;依次类推,可得:第n次共用去卡片2n张,可以看成水平方向n张,竖直方向n张.由此得到第10次共用去卡片20张,前10次共用去的卡片=2(1+2+3+……+9+10),计算即可.
(2)根据2+4+6+8+……+2n表示摆完第n次后共用去的卡片数.由图形可知:这些卡片共有n(n+1)张,即可得到结论;
(3) 用前100次用去的卡片数-前50次共用去的卡片数即可得到结论.
(1)观察图形可知:第1次共用去卡片2张,可以看成水平方向1张,竖直方向1张;
第2次共用去卡片4张,可以看成水平方向2张,竖直方向2张;
第3次共用去卡片6张,可以看成水平方向3张,竖直方向3张;
……
第n次共用去卡片2n张,可以看成水平方向n张,竖直方向n张.
由此得到第10次共用去卡片20张,前10次共用去卡片=2(1+2+3+……+9+10)=![]() =110.
=110.
故答案为:20,110.
(2)2+4+6+8+……+2n=n(n+1).
因为2+4+6+8+……+2n表示摆完第n次后共用去的卡片数.
根据图形可知:这些卡片共有n(n+1)张,
所以2+4+6+8+……+2n= n(n+1).
(3) 摆完第50次共用去50×(50+1)块卡片;
摆完第100次共用去100×(100+1)块卡片;
从第51次至第100次所摆卡片的数量之和为:
100×(100+1)-50×(50+1)=7550.
答:从第51次至第100次所摆卡片的数量之和7550.