题目内容
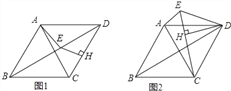
【题目】在四边形OABC中,AB∥OC,∠OAB=90°, ∠OCB=60°,AB=2,OA=2![]() .
.
(1)如图①,连接OB,请直接写出OB的长度;
(2)如图②,过点O作OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒,△OPQ的面积为S(平方单位).
①求S与t之间的函数关系式;
②设PQ与OB交于点M,当△OPM为等腰三角形时,试求出△OPQ的面积S的值.

【答案】(1)4(2);①S=-![]() t2+
t2+![]() t(0<t<2
t(0<t<2![]() ); ②
); ②![]() 或2.
或2.
【解析】试题分析:(1)利用勾股定理即可得;
(2)①首先表示出线段PO,作PE⊥OA于点E,利用锐角三角函数表示出线段PE的长,然后利用三角形的面积计算方法得到有关S于t的函数关系式即可;
②分情况讨论即可得.
试题解析:(1)∵∠OAB=90°,∴OB=![]() ;
;
(2)①∵AB=2,OB=4,∠OAB=90°,∴∠ABO=60°,又∵∠OCB=60°,
∴△BOC为等边三角形,∴OH=OBcos30°=4×![]() =2
=2![]() ,
,
∴OP=OH-PH=2![]() -t,
-t,
如图①,过P点作PE⊥OA,垂足为点E,
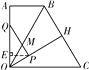
图①
则EP=OPcos30°=3-![]() t,
t,
∴S=![]() ·OQ·EP=
·OQ·EP=![]() ·t·(3-
·t·(3-![]() t)=-
t)=-![]() t2+
t2+![]() t(0<t<2
t(0<t<2![]() );
);
②若△OPM为等腰三角形:
(ⅰ)若OM=PM,如图②,则∠MPO=∠MOP=∠POC,
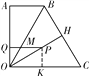
图②
∴PQ∥OC,过点P作PK⊥OC于点K,
∴OQ=PK=![]() ,即t=
,即t=![]() -
-![]() ,解得t=
,解得t=![]() ,
,
此时S=-![]() ×(
×(![]() )2+
)2+![]() ×
×![]() =
=![]() ;
;
(ⅱ)若OP=OM,如图③,则∠OPM=∠OMP=75°,
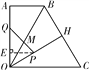
图③
∴∠OQP=∠OMP-∠QOM=75°-30°=45°,此时EQ=EP,即t-(![]() -
-![]() )=3-
)=3-![]() t,
t,
解得t=2,
此时S=-![]() ×22+
×22+![]() ×2=3-
×2=3-![]() ;
;
(ⅲ)若OP=PM,∠POM=∠PMO=∠AOB,
则PQ∥OA,此时点Q在AB上,不满足题意,舍去,
综上所述,当△OPM为等腰三角形时,△OPM的面积为![]() 或2.
或2.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.

【题目】滴滴公布了新的滴滴快车计价规则,车费由“总里程费+总时长费”两部分构成,不同时段收费标准不同,具体收费标准如下表,如果车费不足起步价,则按起步价收费.
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00-10:00 | 1.80 | 0.80 | 14.00 |
10:00-17:00 | 1.45 | 0.40 | 13.00 |
17:00-21:00 | 1.50 | 0.80 | 14.00 |
21:00-6:00 | 0.80 | 0.80 | 14.00 |
(1)小明早上7:10乘坐滴滴快车上学,行车里程6千米,行车时间10分钟,则应付车费多少元?
(2)小云17:10放学回家,行车里程2千米,行车时间12分钟,则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家,20:45在学校上车,由于堵车,平均速度是![]() 千米/小时,15分钟后走另外一条路回家,平均速度是
千米/小时,15分钟后走另外一条路回家,平均速度是![]() 千米/小时,10分钟后到家,则他应付车费多少元?
千米/小时,10分钟后到家,则他应付车费多少元?