题目内容
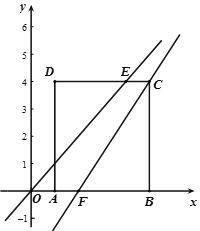
【题目】将边长为4的正方形ABCD置于平面直角坐标系中,使AB边落在x轴的正半轴上且A点的坐标是![]() ,直线y=x与线段CD交于点E.
,直线y=x与线段CD交于点E.
(1)直线![]() 经过点C且与
经过点C且与![]() 轴交于点F.求四边形AFCD的面积.
轴交于点F.求四边形AFCD的面积.
(2)若直线![]() 经过点E和点F,求直线
经过点E和点F,求直线![]() 的解析式.
的解析式.
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,将(2)中直线
平行,将(2)中直线![]() 沿着
沿着![]() 轴向上平移1个单位得到直线
轴向上平移1个单位得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点M,交直线
轴于点M,交直线![]() 于点N,求
于点N,求![]() 的面积.
的面积.
【答案】(1)S梯形AFCD=10;(2)![]() ;(3)S△NMG=3.9.
;(3)S△NMG=3.9.
【解析】
(1)先求出点F的坐标,继而可求出AF的长,然后判断四边形AFCD为直角梯形,进一步即可求出结果;
(2)先求出点E坐标,再利用待定系数法求解即可;
(3)先利用待定系数法求出直线![]() 的函数解析式,再利用平移规律求出直线
的函数解析式,再利用平移规律求出直线![]() 的解析式,然后可求出点M、N的坐标,再利用
的解析式,然后可求出点M、N的坐标,再利用![]() 即可求出结果.
即可求出结果.
解:(1)对于直线![]() ,令y=0,得x=2,∴F(2,0) ,
,令y=0,得x=2,∴F(2,0) ,
∵A(1,0) ,∴AF=1
由题意得:AB=BC=CD=DA=4,AB∥CD,AD⊥AB,
∴ 四边形AFCD为直角梯形,
∴![]() ;
;
(2) 对于直线![]() ,令y=4,得x=4,∴E(4,4) ,
,令y=4,得x=4,∴E(4,4) ,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
将点E、F代入解得:![]() ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
(3)因为直线![]() 与直线y=-3x平行,可设直线
与直线y=-3x平行,可设直线![]() 解析式为
解析式为![]() ,
,
将点![]() 代入,得
代入,得![]() ,解得
,解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
令y=0,解得x=![]() ,∴点H
,∴点H![]() ,
,
∵将直线![]() 沿着
沿着![]() 轴向上平移1个单位得到直线
轴向上平移1个单位得到直线![]() ,
,
∴直线![]() 的解析式的为
的解析式的为![]() ,
,
令y=0,解得x=![]() ,∴点M
,∴点M ![]() .
.
联立 ,解得
,解得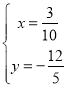 ,∴点N
,∴点N![]() ,
,
∴![]()
![]()
![]()
![]() .
.


练习册系列答案
相关题目