题目内容
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
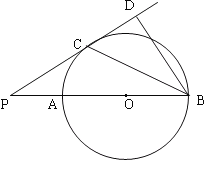
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
【答案】见解析
【解析】试题分析:(1)连接OC.可发现∠OCB和∠DBC同为∠DCB的余角,而∠OCB=∠OBC,由此可得∠OBC=∠DBC,即BC平分∠PBD;
(2)连接AC.证明△ABC∽△CBD即可.
【解答】证明:(1)连接OC.(1分)
∵PD切⊙O于点C,
又∵BD⊥PD,
∴OC∥BD.
∴∠1=∠3.(2分)
又∵OC=OB,
∴∠2=∠3.(3分)
∴∠1=∠2,即BC平分∠PBD.(4分)
(2)连接AC.
∵AB是⊙O的直径,
∴∠ACB=90°.(5分)
又∵BD⊥PD,
∴∠ACB=∠CDB=90°(6分)
又∵∠1=∠2,
∴△ABC∽△CBD;(7分)
∴![]() ,∴BC2=ABBD.(8分)
,∴BC2=ABBD.(8分)

练习册系列答案
相关题目