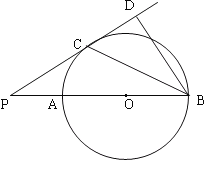
[题目]如图.从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC．(1)求这个扇形的面积,(2)若将扇形BAC围成一个圆锥的侧面.这个圆锥的底面直径是多少?能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC．

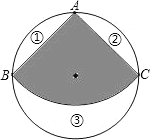
（1）求这个扇形的面积；

（2）若将扇形BAC围成一个圆锥的侧面，这个圆锥的底面直径是多少？能否从最大的余料③中剪出一个圆做该圆锥的底面？请说明理由．

【答案】（1）S扇形=；（2）不能，见解析

【解析】

试题分析：（1）由勾股定理求扇形的半径，再根据面积公式求值；

（2）利用底面周长等于展开图的弧长，可求得直径的长度，进而比较圆锥的底面半径和图中EF的大小关系即可．

解：（1）∵∠A为直角，

∴直径BC=2，

∴根据勾股定理得：AB2+AC2=BC2，

∵AB=AC，

∴AB2+AB2=22，

∴扇形半径为AB=；

∴S扇形=；

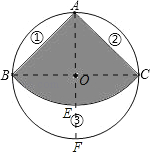
（2）设围成圆锥的底面半径为r，则2πr=，解得；

延长AO分别交弧BC和⊙O于E、F，而EF=2＜；

∴不能从最大的余料③中剪出一个圆做该圆锥的底面．

练习册系列答案

（1）二月份销售收入为_______万元。三月份销售收入为______万元。

（2）二月份男女服装的销售收入分别是多少万元？

【题目】如图，△ABC是边长为4cm的等边三角形，AD为BC边上的高，点P沿BC向终点C运动，速度为1cm/s，点Q沿CA、AB向终点B运动，速度为2cm/s，若点P、Q两点同时出发，设它们的运动时间为x（s）．

（l）求x为何值时，PQ⊥AC；x为何值时，PQ⊥AB？

（2）当O＜x＜2时，AD是否能平分△PQD的面积？若能，说出理由；

（3）探索以PQ为直径的圆与AC的位置关系，请写出相应位置关系的x的取值范围（不要求写出过程）．

【题目】某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

（1）若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；

（2）若降价的最小单位为1元，则当降价多少元时，每星期的利润最大？最大利润是多少？

【题目】某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．

（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；

（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？

（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本＝每件的成本×每天的销售量）

【题目】如图，四边形是的内接矩形，如果的高线长，底边长，设，，

（1）求关于的函数关系式；

（2）当为何值时，四边形的面积最大？最大面积是多少？

【题目】如图，已知抛物线经过点A(－1,0)、B(3,0)、C(0,3)三点。

(1)求抛物线的解析式。

(2)点M是线段BC上的点（不与B，C重合），过M作MN∥y轴交抛物线于N若点M的横坐标为m，请用m的代数式表示MN的长。

(3)在（2）的条件下，连接NB、NC，是否存在m，使△BNC的面积最大？若存在，求m的值；若不存在，说明理由。

【题目】已知：如图，AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC。

求证：（1）BC平分∠PBD；

（2）BC2=AB·BD。

【题目】托车生产是我市的支柱产业之一，不少品牌的摩托车畅销国内外，下表是摩托车厂今年1至5月份摩托车销售量的统计表：（单位：辆）

月份	1	2	3	4	5
销售量（辆）	1700	2100	1250	1400	1680

则这5个月销售量的中位数是辆。

试题分类