题目内容
【题目】随着私家车拥有量的增加,停车问题已经给人们的生活带来了很多不便.为了缓解停车矛盾,某小区开发商欲投资16万元,建造若干个停车位,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的3倍.据测算,建造费用及年租金如下表:
类别 | 室内车位 | 露天车位 |
建造费用(元/个) | 5 000 | 1 000 |
年租金(元/个) | 2 000 | 800 |
(1)该开发商有哪几种符合题意的建造方案?写出解答过程.
(2)若按表中的价格将两种车位全部出租,哪种方案获得的年租金最多?并求出此种方案的年租金.(不考虑其他费用)
【答案】解:(1)设建造室内停车位为x个,则建造露天停车位为![]() 个.
个.
根据题意,得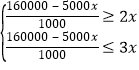
解得20≤x≤![]() .
.
∵x为整数,
∴x取20,21,22.
∴![]() 取60,55,50.
取60,55,50.
∴共有三种建造方案.
方案一:室内停车位20个,露天停车位60个;
方案二:室内停车位21个,露天停车位55个;
方案三:室内停车位22个,露天停车位50个.
(2)设年租金为w元.
根据题意,得
w=2 000x+800![]()
=﹣2 000x+128 000.
∵k=﹣2 000<0,
∴w随x的增大而减小.
∴当x=20时,
w最大=﹣2 000×20+128 000
=88 000(元).
答:当建造室内停车位20个,露天停车位60个时租金最多,最多年租金为88 000元.
【解析】(1)首先设建造室内停车位为x个,则建造露天停车位为:(160000﹣5000x)÷1000个,根据题目中的中的关键语句:①露天车位的数量不少于室内车位的2倍,但不超过室内车位的3倍列出不等式组,然后解出解集后取整数解即可;
(2)设年租金为w元,根据题意可得:室内车位的数量×2000+露天车位的数量×800,可得到w与x的关系表达式,再根据一次函数的增减性确定x的值,求出年租金.
【考点精析】利用一元一次不等式组的应用对题目进行判断即可得到答案,需要熟知1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.

 阅读快车系列答案
阅读快车系列答案【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA , yB .
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= n= 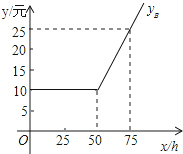
(2)写出![]() 与x之间的函数关系式.
与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?




