题目内容
【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
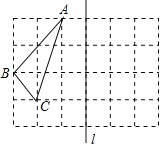
(1)△ABC的形状是 .
(2)利用网格线画△A′B′C′,使它与△ABC关于直线l对称.
(3)在直线l上求作点P使AP+CP的值最小,则AP+CP的最小值= .
【答案】(1)直角三角形;(2)见解析;(3)3![]() .
.
【解析】
(1)直接利用勾股定理以及勾股定理的逆定理,得出三边平方关系式分析得出答案;
(2)直接利用关于直线对称点的性质得出对应点位置,连线即得答案;
(3)直接利用对称点,两点之间线段最短的求最短路线方法得出答案.
(1)∵BC2=12+12=2,
AB2=22+22=8,
AC2=12+32=10,
∴AB2+BC2=AC2,
∴△ABC是直角三角形;
故答案为:直角三角形;
(2)如图所示:作点对称,连线即得△A′B′C′即为所求;
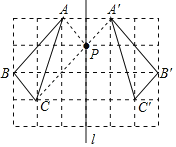
(3)根据两点之间线段最短,作出点A的对称点A′ ,连接A′C交直线l于点P,如图所示:点P即为所求,AP+CP的最小值=A′C=![]() =3
=3![]() .
.
故答案为:3![]() .
.

练习册系列答案
相关题目