题目内容
下列命题中,正确的是
| A.平面上三个点确定一个圆 | B.等弧所对的圆周角相等 |
| C.平分弦的直径垂直于这条弦 | D.与某圆一条半径垂直的直线是该圆的切线 |
C
根据确定圆的条件,切线的判定、圆周角定理及垂径定理,结合题意即可得出答案.
解答:解:A 不在同一直线的三点确定一个圆,没有限制不在同一直线上这个条件,故此项错误;
B在同圆和等圆中,等弧所对的圆周角相等,没有说明在同圆和等圆中这个条件,故此项错误;
C平分弦的直径垂直于弦,此项正确.
D经过半径外端且垂直于这条半径的直线是圆的切线,没有说明经过半径外端这个条件,故此项错误;
故选C.
解答:解:A 不在同一直线的三点确定一个圆,没有限制不在同一直线上这个条件,故此项错误;
B在同圆和等圆中,等弧所对的圆周角相等,没有说明在同圆和等圆中这个条件,故此项错误;
C平分弦的直径垂直于弦,此项正确.
D经过半径外端且垂直于这条半径的直线是圆的切线,没有说明经过半径外端这个条件,故此项错误;
故选C.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目

 ,求BE的长.
,求BE的长.

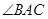 ,
,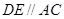 ,且
,且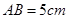 ,求DE的长.
,求DE的长.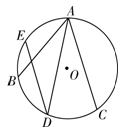
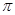 ㎝2
㎝2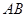 =10米,净高
=10米,净高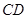 =7米,则此圆的半径
=7米,则此圆的半径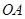 =( )
=( )