Question

【题目】如图，矩形ABCD中，AB＝4，BC＝8，P，Q分别是BC，AB上的两个动点，AE＝2，△AEQ沿EQ翻折形成△FEQ，连接PF，PD，则PF+PD的最小值是(　　)

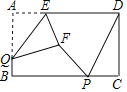
A.10B.9C.8D.7

Answer 1

【答案】C

【解析】

作点D关于BC的对称点D′，连接PD′，ED′，证得DP＝PD′，推出PD+PF＝PD′+PF，又EF＝EA＝2是定值，即可推出当E、F、P、D′四点共线时，PF+PD′定值最小，最小值＝ED′﹣EF即可得出结果．

作点D关于BC的对称点D′，连接PD′，ED′，如图所示：

∵矩形ABCD中，AB＝4，BC＝8，AE＝2，

∴DE＝AD﹣AE＝BC﹣AE＝6，DD′＝2DC＝2AB＝8，

∴ED′＝ ＝ ＝10，

在△PCD和△PCD′中， ，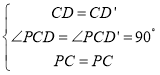

∴△PCD≌△PCD′(SAS)，

∴DP＝PD′，

∴PD+PF＝PD′+PF，

∵EF＝EA＝2是定值，

∴当E、F、P、D′四点共线时，PF+PD′定值最小，最小值＝10﹣2＝8，

∴PF+PD的最小值为8，

故选：C．