题目内容
若|x-
| +(2y+1)2=0,则x2+y2的值是( )
| 1 |
| 2 |
分析:根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可求解.
解答:解:根据题意得,x-
=0,2y+1=0,
解得x=
,y=-
,
∴x2+y2=(
)2+(-
)2=
+
=
.
故选B.
| 1 |
| 2 |
解得x=
| 1 |
| 2 |
| 1 |
| 2 |
∴x2+y2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
故选B.
点评:本题考查了绝对值非负数,平方数非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0列式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
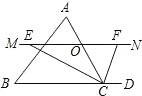 (2013•南漳县模拟)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
(2013•南漳县模拟)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F