题目内容
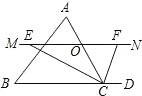 (2013•南漳县模拟)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
(2013•南漳县模拟)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F(1)若CE=12,CF=5,求OC的长;
(2)当点O在边AC上运动到何处且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
分析:(1)利用角平分线的性质以及平行线的性质得出OE=OF,进而利用勾股定理求出EF的长,即可得出CO的长;
(2)利用平行四边形及矩形的性质和判定证明四边形AECF是正方形.
(2)利用平行四边形及矩形的性质和判定证明四边形AECF是正方形.
解答:解:(1)∵OF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠ECD,
∴∠OFC=∠COF,
∴OF=OC,
∴OE=OF;
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
∴∠ECF=90°,
∵CE=12,CF=5,
∴EF=
=13,
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∴CO是△ECF上的中线,
∴CO=
EF=6.5;
(2)点O是AC的中点且∠ACB=90°,
理由:∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴?AECF为矩形,
又∵AC⊥EF.
∴?AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠ECD,
∴∠OFC=∠COF,
∴OF=OC,
∴OE=OF;
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F
∴∠ECF=90°,
∵CE=12,CF=5,
∴EF=
| 122+52 |
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∴CO是△ECF上的中线,

∴CO=
| 1 |
| 2 |
(2)点O是AC的中点且∠ACB=90°,
理由:∵O为AC中点,
∴OA=OC,
∵由(1)知OE=OF,
∴四边形AECF为平行四边形;
∵∠1=∠2,∠4=∠5,∠1+∠2+∠4+∠5=180°,
∴∠2+∠5=90°,即∠ECF=90°,
∴?AECF为矩形,
又∵AC⊥EF.
∴?AECF是正方形.
∴当点O为AC中点且△ABC是以∠ACB为直角三角形时,四边形AECF是正方形.
点评:本题考查的是平行线、角平分线、正方形、平行四边形的性质与判定,涉及面较广,在解答此类题目时要注意角的运用,一般通过角判定一些三角形,多边形的形状,需同学们熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•南漳县模拟)如图,△ABC中,AB=AC,∠BAC=100°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数为( )
(2013•南漳县模拟)如图,△ABC中,AB=AC,∠BAC=100°,把△ABC绕点A逆时针旋转20°得到△ADE(点D与点B是对应点,点E与点C是对应点),连接CE,则∠CED的度数为( )