题目内容
附加题:在平面直角坐标系中,直线y=-| 1 |
| 2 |
(1)若k=
| 1 |
| 2 |
(2)若△OAB的面积是5,求此时点A的坐标及k的值(图(2)备用)
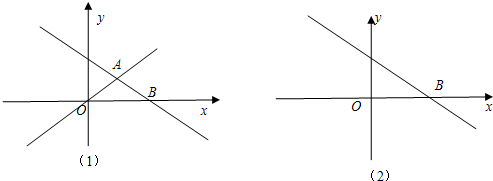
分析:(1)首先求出正比例函数y=kx的解析式,再将两函数式联立,组成二元一次方程组,即可求出A点的坐标;利用平行四边形的性质得出平行四边形第四个顶点的坐标,坐标点应该有三个.
(2)利用直线y=-
x+5与x轴交于B点,求出B点的坐标,再结合三角形的面积为5,求出三角形的高,即是A点的纵坐标,代入
代入y=kx,即可求出k的值.
(2)利用直线y=-
| 1 |
| 2 |
代入y=kx,即可求出k的值.
解答: 解:(1)①把k=
解:(1)①把k=
代入y=kx中得:y=
x,
两函数解析式联列,
,
解方程组得:
,
∴点A的坐标为(5,
),
②这个平行四边形第四个顶点的坐标分别为(15,
),(-5,
),(5,-
);
(2)∵直线y=-
x+5与x轴交于B点,
∴-
x+5=0,
∴B点的坐标为:(10,0),
∴BO=10,
当△OAB的面积是5时,
S△=
OB×h=
×10×h=5,
∴h=1,把h=1,代入y=-
x+5,
即h=y=-
x+5,
解得:x=8,
此时点A的坐标为(8,1);
将A的坐标(8,1)代入y=kx
解得:y=
x.
即:k=
.
 解:(1)①把k=
解:(1)①把k=| 1 |
| 2 |
| 1 |
| 2 |
两函数解析式联列,
|
解方程组得:
|
∴点A的坐标为(5,
| 5 |
| 2 |
②这个平行四边形第四个顶点的坐标分别为(15,
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
(2)∵直线y=-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
∴B点的坐标为:(10,0),
∴BO=10,
当△OAB的面积是5时,
S△=
| 1 |
| 2 |
| 1 |
| 2 |
∴h=1,把h=1,代入y=-
| 1 |
| 2 |
即h=y=-
| 1 |
| 2 |
解得:x=8,
此时点A的坐标为(8,1);
将A的坐标(8,1)代入y=kx
解得:y=
| 1 |
| 8 |
即:k=
| 1 |
| 8 |
点评:此题主要考查了一次函数解析式的求法,以及两一次函数交点坐标的求法和平行四边形的性质,还有三角形的面积公式等知识.

练习册系列答案
相关题目
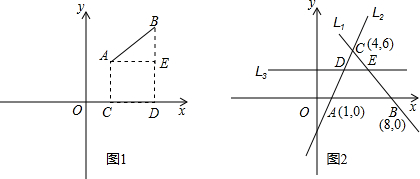
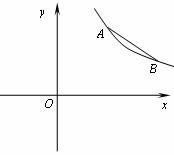
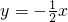 +5与x轴交于B点,与正比例函数y=kx(k≠0)的图象交于第一象限内的点A(如图(1))
+5与x轴交于B点,与正比例函数y=kx(k≠0)的图象交于第一象限内的点A(如图(1)) 时,①求点A的坐标;②以O、A、B三点为顶点在图(1)中画出平行四边形,并直接写出平行四边形第四个顶点的坐标;
时,①求点A的坐标;②以O、A、B三点为顶点在图(1)中画出平行四边形,并直接写出平行四边形第四个顶点的坐标;
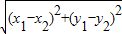 ,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|
,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|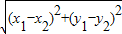 (因为|AB|表示线段长,为非负数)
(因为|AB|表示线段长,为非负数) ,求线段|DA|的长.
,求线段|DA|的长.