题目内容
9、AB、AC为⊙O相等的两弦，弦AD交BC于E，若AC=12，AE=8，则AD=
18
．分析：画出图形，连接BD，根据已知条件，易证△ABE∽△ADB，所以AB2=AE•AD，可求得AD=18．
解答：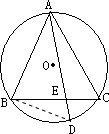
解：连接BD，
∵AB=AC，
∴∠ABC=∠ACB，
∵∠ADB=∠ACB，
∴∠ABC=∠ADB，
又∵∠BAD=∠EAB，
∴△ABE∽△ADB，
∴AB2=AE•AD，
∵AC=12，AE=8，
∴AD=18．
故答案为18．
解：连接BD，∵AB=AC，
∴∠ABC=∠ACB，
∵∠ADB=∠ACB，
∴∠ABC=∠ADB，
又∵∠BAD=∠EAB，
∴△ABE∽△ADB，
∴AB2=AE•AD，
∵AC=12，AE=8，
∴AD=18．
故答案为18．
点评：本题考查了相似三角形的性质和判定，圆中有关定理为证明角相等提供了条件，从而相似的证明与应用常常与圆结合起来．
练习册系列答案
学业测评一课一测系列答案
相关题目
