Question

【题目】如图1，在△ABC中，∠A的外角平分线交BC的延长线于点D．

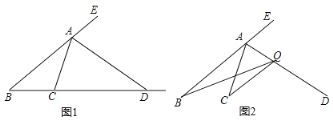
（1）线段BC的垂直平分线交DA的延长线于点P，连接PB，PC．

①利用尺规作图补全图形1，不写作法，保留痕迹；

②求证：∠BPC=∠BAC；

（2）如图2，若Q是线段AD上异于A，D的任意一点，判断QB+QC与AB+AC的大小，并予以证明．

Answer 1

【答案】（1）①如图1所示，见解析；②证明见解析；（2）QB+QC＞AB+AC．证明见解析.

【解析】

（1）①作出线段BC的垂直平分线即可；

②在AE上截取AF=AC．设PC交AB于G．由△APC≌△APF，推出∠PCA=∠PFA，PC=PF，由点P在线段BC的垂直平分线上，推出PB=PC=PF，推出∠PBF=∠PFA，推出∠PBG=∠ACG，由∠PGB=∠AGC，可得∠BPC=∠BAC；

（2）如图2中，在AE上截取AF=AC．可得△QAF≌△QAC解决问题；

（1）①解：如图1所示，

②证明：在AE上截取AF=AC．设PC交AB于G．

∵AD平分∠CAF，

∴∠DAC=∠DAF，

∴∠CAP=∠FAP，

∵AP=AP，AC=AF，

∴△APC≌△APF，

∴∠PCA=∠PFA，PC=PF，

∵点P在线段BC的垂直平分线上，

∴PB=PC=PF，

∴∠PBF=∠PFA，

∴∠PBG=∠ACG，

∵∠PGB=∠AGC，

∴∠BPC=∠BAC；

（2）如图2中，在AE上截取AF=AC．

同法可证△QAF≌△QAC，

∴QC=QF，

∵QB+QC=QB+QF＞BF，BF=AB+AF=AB+AC，

∴QB+QC＞AB+AC．