题目内容
【题目】如图，在平面直角坐标系中，点A和点B的坐标分别为A（4，0）、B（0，2），将△ABO绕点P（2，2）顺时针旋转得到△OCD，点A、B和O的对应点分别为点O、C和D，
（1）画出△OCD，并写出点C和点D的坐标；
（2）连接AC，在直线AC的右侧取点M，使∠AMC=45°，
①若点M在x轴上，则点M的坐标为 ；
②若△ACM为直角三角形，求点M的坐标；
（3）若点N满足∠ANC＞45°，请确定点N的位置（不要求说明理由）.
【答案】(1)画图详见解析；C（2，4），D（0，4）；(2)①（6，0）；②点M的坐标为（8，2）或（6，6）；(3)点N在以点（5，3）或点（1，1）为圆心，以
为半径的圆内．
【解析】
试题分析：（1）先确定出OA，OB，再由旋转的性质得出OD=4，CD=2，即可得出结论；
（2）先构造出满足条件的点M的位置，利用等腰三角形的性质和等腰直角三角形的性质即可得出结论；
（3）同（2）①的方法得出结论．
试题解析：（1）如图1，
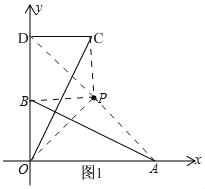
∵点A和点B的坐标分别为A（4，0）、B（0，2），
∴OA=4，OB=2，
由旋转知，△POD≌△PAO，△PCD≌△PBO，
∴OD=OA=4，CD=OB=2，
∴C（2，4），D（0，4）；
（2）①如图2，
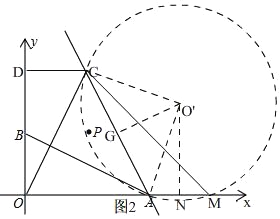
∵A（4，0），C（2，4），
∴AC=
，
以AC为斜边在直线AC右侧作等腰直角三角形ACO′，以O′为圆心，O′A为半径作圆，
∴∠AMC=
∠AO′C=45°，
过点O′作O′G⊥AC，
∵A（4，0），C（2，4），
∴G（3，2），
∴直线AC的解析式为y=﹣2x+8，
∴直线O′G的解析式为y=
，
设点O′的坐标为（m，
），
∴
=
=
，
∴m=5或m=1（点O′在直线AC右侧，所以舍去），
∴O′（5，3），
∴O′A=
，
在Rt△AO′N中，O′N=3，AN=
=1，
∴AM=2AN=2，
∴M（6，0）；
故答案为:（6，0），
②如图3，
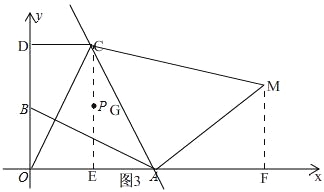
当∠CAM为直角时，
分别过点C，M作x轴的垂线，垂足分别为E，F．
∵CO=CA，
∴OE=AE=
OA=2，
∴∠CAE+∠ACE=90°，
∵∠CAE+∠FAM=90°，
∴∠ACE=∠FAM，
在△ACE和△MAF中∠AEC=∠MFA，∠ACE=∠FAM，AC=AM，
∴△CEA≌△AFM，
∴MF=AE=2，AF=CE=4，
∴OF=8，
∴M（8，2）；
当∠ACM为直角时，
同理可得M（6，6）；
综上所述，点M的坐标为（8，2）或（6，6）．
（3）如图3，
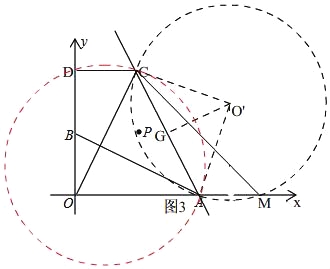
∵A（4，0），C（2，4），
∴AC=
，
以AC为斜边在直线AC右侧作等腰直角三角形ACO′，以O′为圆心，O′A为半径作圆，
∴∠ANC＜
∠AO′C=45°，
过点O′作O′G⊥AC，
∵A（4，0），C（2，4），
∴G（3，2），直线AC的解析式为y=﹣2x+8，
∴直线O′G的解析式为y=，
设点O′的坐标为（m，），
∴==，
∴m=5或m=1，
∴O′（5，3）或（1，1），
∵A（4，0），
∴O′A=，
∴点N在以点（5，3）或点（1，1）为圆心，以为半径的圆内．
