题目内容
【题目】如图,正方形ABCD的面积为4,点F,G分别是AB,DC的中点,将点A折到FG上的点P处,折痕为BE,点E在AD上,则AE长为______.
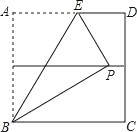
【答案】![]()
【解析】
利用正方形ABCD的面积为4得到正方形ABCD的边长为2,再根据折叠的性质得BA=BP=2,∠ABE=∠PBE;由于点F,G分别是AB,DC的中点,则FG⊥AB,BF=1,在Rt△BPF中,由于PB=4,BF=2,根据含30度的直角三角形三边的关系得到得到∠FPB=30°,利用互余得∠ABP=60°,则∠ABE=30°,然后在Rt△ABE中根据含30度的直角三角形三边的关系求AE的长.
如图,
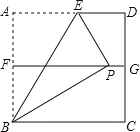
∵正方形ABCD的面积为4,
∴正方形ABCD的边长为2,
∵点A折到FG上的点P处,折痕为BE,
∴BA=BP=2,∠ABE=∠PBE,
∵点F,G分别是AB,DC的中点,
∴FG⊥AB,BF=1,
在Rt△BPF中,PB=4,BF=2,
∴∠FPB=30°,
∴∠ABP=60°,
∴∠ABE=30°,
在Rt△ABE中,AE=![]() AB=
AB=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目