题目内容
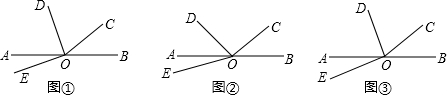
如图.D为直线AB上一点,∠BOC=α.
(1)如图①,若α=40°,OD平分∠AOC,∠DOE=90°,则∠AOE=
(2)如图②,若∠AOD=
∠AOC,∠DOE=60°,请用α表示∠AOE的度数;
(3)如图③,∠AOD=
∠AOC,∠DOE=
(n≥2,且n为正整数),请用α和n表示∠AOE的度数.
(直接写出结果)
(1)如图①,若α=40°,OD平分∠AOC,∠DOE=90°,则∠AOE=
20°
20°
;(2)如图②,若∠AOD=
| 1 |
| 3 |
(3)如图③,∠AOD=
| 1 |
| n |
| 180° |
| n |
(直接写出结果)

分析:(1)利用角平分线的性质得出∠AOD=∠DOC=70°,进而得出∠AOE的度数;
(2)利用设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,得出x的值,进而用α表示∠AOE的度数;
(3)利用(2)中作法,得出x与α的关系,进而得出答案.
(2)利用设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,得出x的值,进而用α表示∠AOE的度数;
(3)利用(2)中作法,得出x与α的关系,进而得出答案.
解答:解:(1)∵∠BOC=40°,OD平分∠AOC,
∴∠AOD=∠DOC=70°,
∵∠DOE=90°,则∠AOE=90°-70°=20°;
故答案为:20°;
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,
解得:x=
,
∴∠AOE=60-x=60-
=
α;
(3)设∠AOD=x,则∠DOC=(n-1)x,∠BOC=180-nx=α,
解得:x=
,
∴∠AOE=
-
=
.
∴∠AOD=∠DOC=70°,
∵∠DOE=90°,则∠AOE=90°-70°=20°;
故答案为:20°;
(2)设∠AOD=x,则∠DOC=2x,∠BOC=180-3x=α,
解得:x=
| 180-α |
| 3 |
∴∠AOE=60-x=60-
| 180-α |
| 3 |
| 1 |
| 3 |
(3)设∠AOD=x,则∠DOC=(n-1)x,∠BOC=180-nx=α,
解得:x=
| 180-α |
| n |
∴∠AOE=
| 180 |
| n |
| 180-α |
| n |
| α |
| n |
点评:此题主要考查了角的计算,正确根据角之间的数量关系得出等式是解题关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=
17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=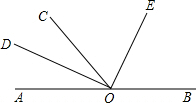 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.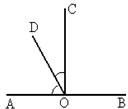 13、如图,O为直线AB上一点,OC平分∠AOB,∠COD=34°20′,则∠AOD=
13、如图,O为直线AB上一点,OC平分∠AOB,∠COD=34°20′,则∠AOD= 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90° 如图,O为直线AB上一点,OC平分∠AOD,3∠AOC=∠BOC,
如图,O为直线AB上一点,OC平分∠AOD,3∠AOC=∠BOC,