题目内容
 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°(1)请你数一数,图中有
9
9
个小于平角的角;(2)求出∠AOD和∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
分析:(1)根据图形数出角的个数即可.
(2)根据角平分线定义求出∠AOD和∠COD,根据平角定义求出∠BOC,即可求出∠BOD.
(3)求出∠COE和∠BOE的度数,即可得出答案.
(2)根据角平分线定义求出∠AOD和∠COD,根据平角定义求出∠BOC,即可求出∠BOD.
(3)求出∠COE和∠BOE的度数,即可得出答案.
解答:解:(1)有∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB,共9个,
故答案为:9.
(2)∵∠AOC=50°,OD平分∠AOC,
∴∠AOD=∠COD=
∠AOC=
×50°=25°,
∵∠AOC=50°,
∴∠BOC=180°-∠AOC=130°,
∵∠COD=25°,
∴∠BOD=∠BOC+∠COD=130°+25°=155°.
(3)∵∠COD=25°,∠DOE=90°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°,
∵∠BCO=130°,
∴∠BOE=∠BOC-∠EOC=130°-65°=65°=∠COE,
即OE平分∠BOC.
故答案为:9.
(2)∵∠AOC=50°,OD平分∠AOC,
∴∠AOD=∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC=50°,
∴∠BOC=180°-∠AOC=130°,
∵∠COD=25°,
∴∠BOD=∠BOC+∠COD=130°+25°=155°.
(3)∵∠COD=25°,∠DOE=90°,
∴∠COE=∠DOE-∠DOC=90°-25°=65°,
∵∠BCO=130°,
∴∠BOE=∠BOC-∠EOC=130°-65°=65°=∠COE,
即OE平分∠BOC.
点评:本题考查了角平分线定义和角的有关计算的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
 17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=
17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=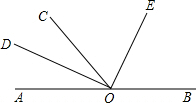 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°. 13、如图,O为直线AB上一点,OC平分∠AOB,∠COD=34°20′,则∠AOD=
13、如图,O为直线AB上一点,OC平分∠AOB,∠COD=34°20′,则∠AOD= 如图,O为直线AB上一点,OC平分∠AOD,3∠AOC=∠BOC,
如图,O为直线AB上一点,OC平分∠AOD,3∠AOC=∠BOC,