题目内容
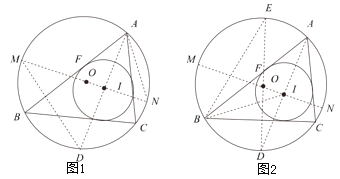
【题目】(感知)小亮遇到了这样一道题:已知如图在![]() 中,
中,![]() 在
在![]() 上,
上,![]() 在
在![]() 的延长上,
的延长上,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
小亮仔细分析了题中的已知条件后,如图②过![]() 点作
点作![]() 交
交![]() 于
于![]() ,进而解决了该问题.(不需要证明)
,进而解决了该问题.(不需要证明)
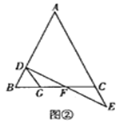
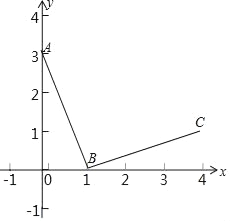
(探究)如图③,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
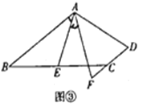
(应用)如图③,在正方形![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 边上的点,若
边上的点,若![]() =1,
=1,![]() =
=![]() ,∠
,∠![]() =90°,则
=90°,则![]() 的长为 .
的长为 .
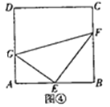
【答案】探究:![]() ;应用:
;应用:![]() .
.
【解析】
探究:分别延长DC、AE,交于点G,根据已知条件可以得到△ABE≌△GCE,由此得到AB=CG,由∠BAE=∠EAF,等量代换可证∠CGE=∠EAF,进而得到AF=GF,即可得出结论;
应用:分别延长FB、GE,交于点H,根据已知条件可以得到△AEG≌△BEH,由此得到AG=BH,GE=HE,然后利用三线合一的性质得到FG=FH,即可求出GF.
解:探究:AB=AF+CF;
证明:如图,分别延长DC、AE,交于点G,

∵AB∥DC,
∴∠BAE=∠CGE,∠ABE=∠GCE,
∵BE=CE,
∴△ABE≌△GCE,
∴AB=CG,
又∵∠BAE=∠EAF,
∴∠CGE=∠EAF,
∴AF=GF,
∴AB=CG=GF+CF=AF+CF;
应用:如图,分别延长FB、GE,交于点H,
∵∠A=∠EBH=90°,∠GEA=∠HEB,AE=BE,
∴△AEG≌△BEH,
∴AG=BH,GE=HE,
又∵∠GEF=90°,即FE⊥GH,
∴FG=FH,
∵FH=BF+BH=BF+AG=![]() ,
,
∴GF=![]() .
.

【题目】已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x | … | 0 |
| 4 | … |
y | … | 0.37 | -1 | 0.37 | … |
则方程ax2+bx+1.37=0的根是( )
A.0或4B.![]() 或
或![]() C.1或5D.无实根
C.1或5D.无实根