题目内容
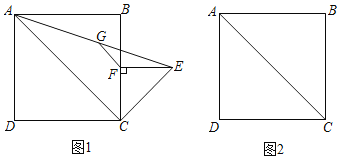
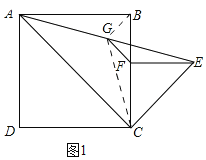
【题目】如图1,在正方形ABCD中,点F在边BC上,过点F作EF⊥BC,且FE=FC(CE<CB),连接CE、AE,点G是AE的中点,连接FG.
(1)用等式表示线段BF与FG的数量关系是 ;
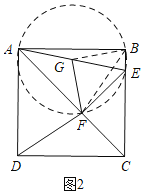
(2)将图1中的△CEF绕点C按逆时针旋转,使△CEF的顶点F恰好在正方形ABCD的对角线AC上,点G仍是AE的中点,连接FG、DF.
①在图2中,依据题意补全图形;
②求证:DF=![]() FG.
FG.
【答案】(1)BF=![]() FG;(2)①如图2所示,见解析;②见解析.
FG;(2)①如图2所示,见解析;②见解析.
【解析】
(1)先判断出△AGB≌△CGB,得到∠GBF=45°,再判断出△EFG≌△CFG,得到∠GFB=45°,从而得到△BGF为等腰直角三角形,即可.
(2)①画图2即可;
②如图2,连接BF、BG,证明△ADF≌△ABF得DF=BF,根据直角三角形斜边中线的性质得:AG=EG=BG=FG,由圆的定义可知:点A、F、E、B在以点G为圆心,AG长为半径的圆上,∠BGF=2∠BAC=90°,所以△BGF是等腰直角三角形,可得结论.
(1)BF=![]() FG,
FG,
理由是:如图1,连接BG,CG,
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=![]() ∠ABC=45°,
∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=![]() (360°﹣∠BFE)=
(360°﹣∠BFE)=![]() (360°﹣90°)=135°,
(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=![]() FG.
FG.
故答案为:BF=![]() FG;
FG;
(2)①如图2所示,
②如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵![]() ,∠BAC=45°,
,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=![]() FG,
FG,
∴DF=![]() FG.
FG.

【题目】二次函数![]() (a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | -1 | 0 | 1 | 3 | … |
y | … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是( )
A.抛物线开口向上B.抛物线与y轴交于负半轴
C.抛物线的顶点为(1,3)D.一元二次方程ax2+bx+c=0的正根在3与4之间