Question

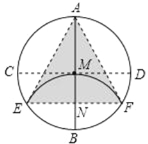
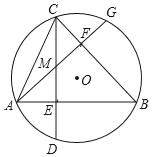
【题目】如图，在圆O中，弦AB⊥CD于E，弦AG⊥BC于F，CD与AG相交于点M．

（1）求证：弧BD=弧BG．

（2）如果AB＝12，CM＝4，求圆O的半径．

Answer 1

【答案】（1）证明见解析；（2）2

【解析】

（1）连结AD、BD、BG，由AB⊥CD，AG⊥BC得到∠CEB=∠AFB=90°，根据等角的余角相等得到∠ECB=∠BAF，即可得出结论；

（2）连接OA、OB、OC、OG、CG，作OH⊥CG于H，OK⊥AB于K，由垂径定理得出CH=GH=CG，AK=BK=AB=6，由圆周角定理和角的互余关系证出∠CNF=∠AGC，得出CG=CM=4，因此GH=2，由AG⊥BC证出弧BG的度数+弧AC的度数=180°，得出∠COG+∠AOB=180°，因此∠HOG+∠BOK=90°，证出∠HGO=∠BOK，由AAS证明△HOG≌△KBO，得出对应边相等OK=HG=2，再由勾股定理求出OB即可．

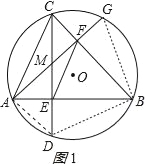
（1）证明：连结AD、BD、BG，如图1所示，

∵AB⊥CD，AG⊥BC，

∴∠CEB＝∠AFB＝90°，

∴∠ECB+∠B＝90°，∠BAF+∠B＝90°，

∴∠ECB＝∠BAF，即∠DCB＝∠BAG，

∴弧BD＝弧BG；

（2）解：连接OA、OB、OC、OG、CG，作OH⊥CG于H，OK⊥AB于K，如图2所示：

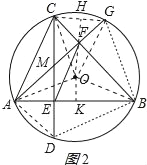
则CH＝GH＝CG，AK＝BK＝AB＝6，

∵∠DCB＝∠BAG，∠DCB+∠CMF＝90°，∠BAG+∠ABF＝90°，

∴∠CMF＝∠ABF，

∵∠ABF＝∠AGC，

∴∠CMF＝∠AGC，

∴CG＝CM＝4，

∴GH＝2，

∵AG⊥BC，

∴∠AFB＝90°，

∴∠FAB+∠FBA＝90°，

∴弧BG的度数+弧AC的度数＝180°，

∴∠COG+∠AOB＝180°，

∴∠HOG+∠BOK＝90°，

∵∠HGO+∠HOG＝90°，

∴∠HGO＝∠BOK，

在△HOG和△KBO中，，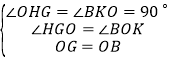

∴△HOG≌△KBO（AAS），

∴OK＝HG＝2，

∴OB＝＝＝2；

即⊙O的半径为2．