题目内容
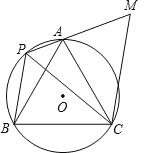
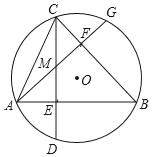
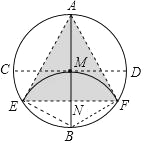
【题目】如图，AB、CD 为圆形纸片中两条互相垂直的直径，将圆形纸片沿EF 折叠，使 B 与圆心 M 重合，折痕 EF 与 AB 相交于 N，连结 AE、AF，得到了以下结论：①四边形 MEBF 是菱形，②△AEF 为等边三角形，③S△AEF：S 圆＝3
：4π，其中正确的是_______．
【答案】①②③
【解析】
①根据垂径定理可得 BM 垂直平分 EF，再求出 BN＝MN，从而得到 BM、EF 互相垂直平分，然后根据对角线互相垂直平分的四边形是菱形求出四边形MEBF 是菱形，从而得到①正确；②连接 ME，根据直角三角形 30°角所对的直角边等于斜边的一半求出∠MEN＝30°，然后求出∠EMN＝60°，根据等边对等角求出∠AEM＝∠EAM，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠AEM ＝30°，从而得到∠AEF＝60°，同理求出∠AFE＝60°，再根据三角形的内角和等于 180°求出∠EAF＝60°，从而判定△AEF 是等边三角形，②正确；③设圆的半径为 r，求出 MN＝
r，EN＝ 
r， 然后求出 AN、EF，再根据三角形的面积公式与圆的公式列式整理即可得到③正确．
①根据垂径定理，BM 垂直平分 EF，
又∵纸片沿 EF 折叠，B、M 两点重合，
∴BN＝MN，
∴BM、EF 互相垂直平分，
∴四边形 MEBF 是菱形，故①正确；
②如图，连接 ME，则 ME＝MB＝2MN．
∵∠ENM＝90°，
∴∠MEN＝30°，
∴∠EMN＝90°﹣30°＝60°，
又∵AM＝ME（都是半径），
∴∠AEM＝∠EAM，
∴∠AEM＝ ∠EMN＝ ×60°＝30°，
∴∠AEF＝∠AEM+∠MEN＝30°+30°＝60°，
同理可求∠AFE＝60°，
∴∠EAF＝60°，
∴△AEF 是等边三角形，故②正确；
③设圆的半径为 r，则 MN＝r，EN＝ r，
∴EF＝2EN＝
r，AN＝r+ r＝
r，
∴S△AEF：S 圆＝（×r×r）：πr2＝3：4，故③正确；
综上所述，结论正确的是①②③．
故答案①②③．
