题目内容
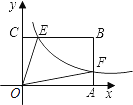
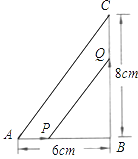
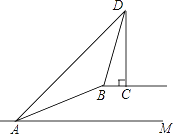
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
【答案】电视塔CD的高度为20m
【解析】
延长DC 交AM于F,作BE⊥AM于E.首先证明四边形BCEF是矩形,由题意BE:AE=1:2.4,在Rt△ABE中,根据AB=26,由勾股定理可得BE=10,AE=24,在Rt△BCD中,可知tan73°=![]() ,推出
,推出![]() ,推出DC=
,推出DC=![]() BC,在Rt△AFD中,由∠DAF=45°,可知AF=DF,可得24+BC=10+
BC,在Rt△AFD中,由∠DAF=45°,可知AF=DF,可得24+BC=10+![]() BC,解方程求出BC即可解决问题.
BC,解方程求出BC即可解决问题.
解:延长DC 交AM于F,作BE⊥AM于E.
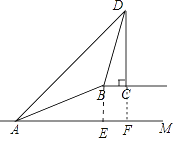
∵DF⊥BC,DF⊥AM,
∴∠AEB=∠AFD=∠DCB=∠BCF=90°,
∴四边形BCEF是矩形,
∴BC=EF,BE=CF,
由题意BE:AE=1:2.4,
在Rt△ABE中,∵AB=26,
由勾股定理可得BE=10,AE=24,
在Rt△BCD中,∵∠DBC=73°,
∴tan73°=![]() ,
,
∴ ![]() ,
,
∴DC= ![]() BC,
BC,
在Rt△AFD中,∵∠DAF=45°,
∴AF=DF,
∴24+BC=10+ ![]() BC,
BC,
∴BC=6,DC=20,
答:电视塔CD的高度为20m

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目