Question

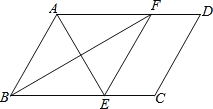
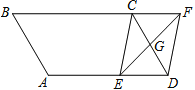
【题目】如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于D，CE⊥DE于点E；

（1）若B、C在DE的同侧（如图所示）且AD=CE．求证：AB⊥AC；

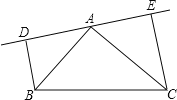
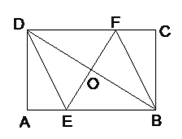
（2）若B、C在DE的两侧（如图所示），其他条件不变，AB与AC仍垂直吗？若是请给出证明；若不是，请说明理由．

Answer 1

【答案】见解析

【解析】

试题分析：（1）由已知条件，证明ABD≌△ACE，再利用角与角之间的关系求证∠BAD+∠CAE=90°，即可证明AB⊥AC；

（2）同（1），先证ABD≌△ACE，再利用角与角之间的关系求证∠BAD+∠CAE=90°，即可证明AB⊥AC．

（1）证明：∵BD⊥DE，CE⊥DE，

∴∠ADB=∠AEC=90°，

在Rt△ABD和Rt△ACE中，

∵，

∴Rt△ABD≌Rt△CAE．

∴∠DAB=∠ECA，∠DBA=∠ACE．

∵∠DAB+∠DBA=90°，∠EAC+∠ACE=90°，

∴∠BAD+∠CAE=90°．

∠BAC=180°﹣（∠BAD+∠CAE）=90°．

∴AB⊥AC．

（2）AB⊥AC．理由如下：

同（1）一样可证得Rt△ABD≌Rt△ACE．

∴∠DAB=∠ECA，∠DBA=∠EAC，

∵∠CAE+∠ECA=90°，

∴∠CAE+∠BAD=90°，即∠BAC=90°，

∴AB⊥AC．