题目内容
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE= ![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )个。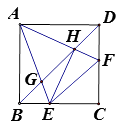
A.2
B.3
C.4
D.5
【答案】D
【解析】①BD是正方形ABCD的对角线,所以∠ABD=45°,
∵∠EAF=45°,∴∠ABD=∠EAF=45°.
∵∠AHB=∠AHG,∴ ![]() ABH∽
ABH∽ ![]() GAH,即①正确。
GAH,即①正确。
②四边形ABCD是正方形,BD为其对角线,所以∠DBC=45°.
∵∠EAF=45°,∴∠EAF=∠DBC.
∴ ![]() AGD∽
AGD∽ ![]() BGE,
BGE, ![]() ,即
,即 ![]()
∵∠AGB=∠HE,∴△ABG∽△HEG.
故②正确.
③由②知△ABG∽△HEG,则∠ABG=∠AEH.
易知∠ABG=45°,所以∠AEH=45°.
∵∠EAH=45°,∴ ![]() AEH是等腰直角三角形.
AEH是等腰直角三角形.
∴ ![]() =
= ![]() ,AE=
,AE= ![]() AH
AH
即③正确.
④由③知 ![]() AEH是等腰直角三角形,所以EH⊥AF,即④正确。
AEH是等腰直角三角形,所以EH⊥AF,即④正确。
⑤将△ADF绕点A顺时针旋转90°得到△ABM.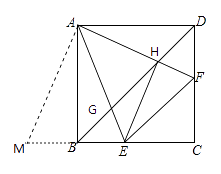
易知BM=DF,∠DAF=∠BAM,AF=AM
四边形ABCD为正方形,∠EAF=45°,则∠BAE+∠DAF=45°
即∠BAM+∠BAE=∠MAE=45°.
∵AE=AE
∴ ![]() AFE≌
AFE≌ ![]() AME,ME=EF.
AME,ME=EF.
∵ME=MB+BE=DF+BE
∴EF=BE+DF。
所以五个命题都是正确,答案为D.
根据相似三角形的判定,证明三角形相似。对于最后一问,注意问题的转化,通过作辅助线,证明ME=EF=EB+DF。

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目