题目内容
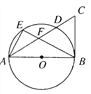
【题目】如图所示,AB是00的直径,BC是⊙O的切线,连接AC,交⊙0于D,E为弧AD上一点,连接AE,BE交AC于点F且![]() ,(1)求证CB=CF;(2)若点E到弦AD的距离为3,cos C=
,(1)求证CB=CF;(2)若点E到弦AD的距离为3,cos C=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)6
【解析】试题分析:(1)如图1,通过相似三角形![]() 的对应角相等推知,
的对应角相等推知,![]() 又由弦切角定理、对顶角相等证得
又由弦切角定理、对顶角相等证得![]() 最后根据等角对等边证得结论;
最后根据等角对等边证得结论;
(2)如图2,连接OE交AC于点G,设![]() 的半径是r.根据(1)中的相似三角形的性质证得∠4=∠5,所以由“圆周角、弧、弦间的关系”推知点E是弧
的半径是r.根据(1)中的相似三角形的性质证得∠4=∠5,所以由“圆周角、弧、弦间的关系”推知点E是弧![]() 的中点,则
的中点,则![]() 然后通过解直角
然后通过解直角![]() 求得
求得![]() ,则以求
,则以求![]() 的值.
的值.
试题解析:(1)证明:如图1,
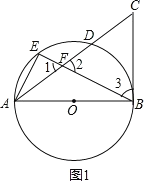
∵![]()
又∵∠AEF=∠AEB,
∴△AEF∽△AEB,
∴∠1=∠EAB.
∵∠1=∠2,∠3=∠EAB,
∴∠2=∠3,
∴CB=CF;
(2)如图2,连接OE交AC于点G,设![]() 的半径是r.
的半径是r.
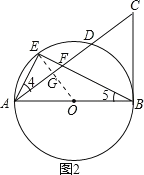
由(1)知,△AEF∽△AEB,则∠4=∠5.
∴.![]() =
=![]() ,
,
∴OE⊥AD,
∴EG=3
![]() 且
且![]()
![]()
![]() 即
即![]()
解得,r=6,即![]() 的半径是6.
的半径是6.

练习册系列答案
相关题目