Question

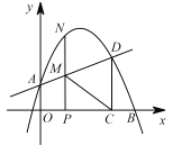
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+1交y轴于点A，交x轴正半轴于点B(4，0) ，与过A点的直线相交于另一点D(3，) ，过点D作DC⊥x轴，垂足为C．

（1）求抛物线的表达式；

（2）点P在线段OC上（不与点O，C重合），过P作PN⊥x轴，交直线AD于M，交抛物线于点N，连接CM，求△PCM 面积的最大值；

（3）若P 是x 轴正半轴上的一动点，设OP 的长为t.是否存在t，使以点M，C，D，N 为顶点的四边形是平行四边形?若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）；（3）详见解析.

【解析】试题分析：（1）把B（4，0），点D（3， ）代入即可得出抛物线的解析式；

（2）先用含t的代数式表示P、M坐标，再根据三角形的面积公式求出△PCM的面积与t的函数关系式，然后运用配方法可求出△PCM面积的最大值；

（3）若四边形DCMN为平行四边形，则有MN=DC，故可得出关于t的二元一次方程，解方程即可得到结论．

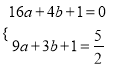试题解析：（1）把点B（4，0），点D（3， ），代入中得， ，解得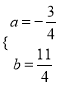： ，∴抛物线的表达式为；

（2）设直线AD的解析式为y=kx+b，∵A（0，1），D（3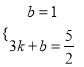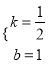， ），∴，∴，∴直线AD的解析式为，设P（t，0），∴M（t， ），∴PM=，∵CD⊥x轴，∴PC=3﹣t，∴S△PCM=PCPM=（3﹣t）（），∴S△PCM==，∴△PCM面积的最大值是；

（3）∵OP=t，∴点M，N的横坐标为t，设M（t， ），N（t， ），∴MN== ，CD=，如果以点M、C、D、N为顶点的四边形是平行四边形，∴MN=CD，即=，∵△=﹣39，∴方程=无实数根，∴不存在t，使以点M、C、D、N为顶点的四边形是平行四边形．

（3）∵OP=t，∴点M，N的横坐标为t，设M（t， ），N（t， ），∴MN== ，CD=；

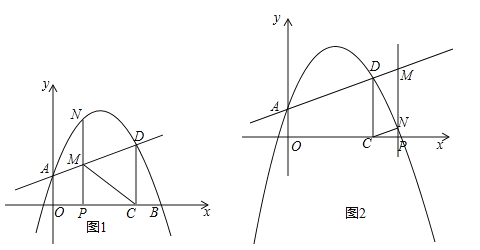
①如图1，如果以点M、C、D、N为顶点的四边形是平行四边形，∴MN=CD，即=，∵△=﹣39，∴方程=无实数根，∴不存在t；

②如图2，如果以点M、C、D、N为顶点的四边形是平行四边形，∴MN=CD，即=，∴t=（负值舍去），∴当t=时，以点M、C、D、N为顶点的四边形是平行四边形．