题目内容
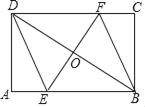
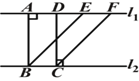
【题目】如图，
∥
，BE∥CF，BA⊥，DC⊥，下面给出四个结论：①BE＝CF；②AB＝DC；③
；
④四边形ABCD是矩形．其中说法正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】分析：由已知可得，四边形BCEF是平行四边形可判断①，四边形ABCD都是矩形可判断②、④；根据等底等高的两个三角形面积相等，可对③进行判断.根据矩形的判定方法可对③判断.
详解：∵
∥
，BE∥CF，
∴四边形BCFE是平行四边形，
∴BE=DF，
故①正确；
∵BA⊥，DC⊥，∥，
∴BA∥DC，
∴四边形ABCD是矩形，
∴AB＝DC；
故②、④正确；
∵四边形BCFE是平行四边形，
∴EF=BC.
∵四边形ABCD是矩形，
∴AD=BC,
∴AD=EF,
∴AE=DF,
∴△ABE和△DCF等底同高，所以面积相等，
故③正确.
故选D.
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
【题目】我们规定：有理数xA用数轴上点A表示，xA叫做点A在数轴上的坐标；有理数xB用数轴上点B表示，xB叫做点B在数轴上的坐标．|AB|表示数轴上的两点A，B之间的距离．
（1）借助数轴，完成下表：
xA | xB | xA﹣xB | |AB| |
3 | 2 | 1 | 1 |
1 | 5 |
|
|
2 | ﹣3 |
|
|
﹣4 | 1 |
|
|
﹣5 | ﹣2 |
|
|
﹣3 | ﹣6 |
|
|
（2）观察（1）中的表格内容，猜想|AB|= ；（用含xA，xB的式子表示，不用说理）
（3）已知点A在数轴上的坐标是﹣2，且|AB|=8，利用（2）中的结论求点B在数轴上的坐标．
