题目内容
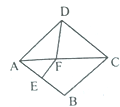
【题目】已知:如图,ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. 
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB=°时,四边形ACED是正方形?请说明理由.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠D=∠OCE,∠DAO=∠E.
∵O是CD的中点,
∴OC=OD,
在△ADO和△ECO中,
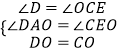 ,
,
∴△AOD≌△EOC(AAS);
(2)45
【解析】(2)当∠B=∠AEB=45°时,四边形ACED是正方形. ∵△AOD≌△EOC,
∴OA=OE.
又∵OC=OD,
∴四边形ACED是平行四边形.
∵∠B=∠AEB=45°,
∴AB=AE,∠BAE=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠COE=∠BAE=90°.
∴ACED是菱形.
∵AB=AE,AB=CD,
∴AE=CD.
∴菱形ACED是正方形.
所以答案是:45.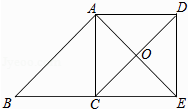
【考点精析】根据题目的已知条件,利用平行四边形的性质和正方形的判定方法的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.

练习册系列答案
相关题目