题目内容
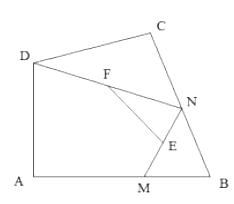
【题目】如图,![]() 中,
中,![]() ,在
,在![]() 的同侧作正
的同侧作正![]() 、正
、正![]() 和正
和正![]() ,则四边形
,则四边形![]() 面积的最大值是( )
面积的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
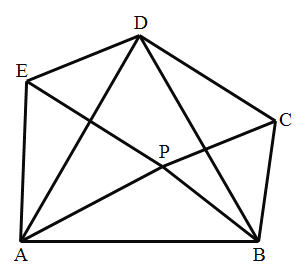
先证△EAD≌△PAB得出DE=BP, 再证△DBC≌△ABP得出DC=AP,由题意△APE和△BPC是等边三角形,可得EP=AP,BP=CP,所以四边形PCDE是平行四边形.CP⊥EP时,四边形面积最大,套入公式计算即可.
解:∵△APE和△ABD是等边三角形,
∴AE=AP=4,AB=AD,∠EAP=∠DAB=60°,∠EAD=∠PAB=60°-∠DAP,
在△EAD和△PAB中
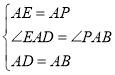
∴△EAD≌△PAB(SAS),
∴DE=BP,
同理△DBC≌△ABP,
∴DC=AP,
∵△APE和△BPC是等边三角形,
∴EP=AP,BP=CP,
∴DE=CP=3,DC=PE=4,
∴四边形PCDE是平行四边形,
当CP⊥EP时,四边形PCDE的面积最大,最大面积是3×4=12,
故选A.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目