题目内容
【题目】在平面直角坐标系中xOy,抛物线y=x2-2(m-1)x+m2-4m+3的顶点为C,直线y=-2x+3与抛物线相交于A、B两点,点A在抛物线的对称轴的左侧.
(1)求点C的坐标(用含m的代数式表示);
(2)若P为直线OC上一动点,求△APB的面积;
(3)当OA+OB的值最小时,求m的值.
【答案】(1)C(m-1,2-2m);(2)△APB的面积=![]() ×4
×4![]() ×
×![]() =6;(3)m的值
=6;(3)m的值![]() .
.
【解析】试题分析:(1)把函数解析式整理成顶点式形式,然后写出点![]() 的坐标;
的坐标;
(2)联立直线与抛物线求出交点![]() 的坐标,然后求出
的坐标,然后求出![]() 的长,再根据AB∥OC求出两平行线间的距离,最后根据三角形的面积公式列式计算即可得解;
的长,再根据AB∥OC求出两平行线间的距离,最后根据三角形的面积公式列式计算即可得解;
![]() 分情况进行讨论即可.
分情况进行讨论即可.
试题解析:(1)抛物线的解析式可化为![]()
![]()
(2)∵直线OC的解析式为![]() ∴AB∥OC.
∴AB∥OC.
令AB与x轴、y轴分别交于点D、K,则![]()
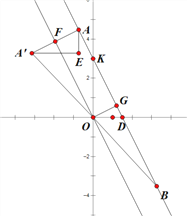
过点O作![]() 于点G,
于点G,
∵![]()
∴![]() ∴OG=
∴OG=![]() .
.
∴AB与OC之间的距离为![]() .
.
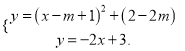
解得: ![]() 或
或![]()
∴![]()
∴![]()
∴![]() 的面积=
的面积=![]() ×4
×4![]() ×
×![]() =6.
=6.
(3)如答图1,设点A关于![]() 的对称点为A′,则
的对称点为A′,则![]()
过点A作AE∥y轴,A′E∥x轴,AE与A′E交于点E, 则可证![]()
∴![]() ,解得
,解得![]()
![]()
1)当点A′在第二象限,由于A′、O、B三点在同一条直线上,B不可能在第一或第二象限.
2)当点A′在第二象限时,点B在第四象限时.
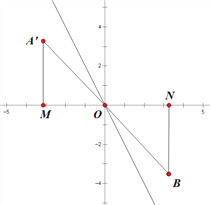
分别过点A′、B作x轴的垂线段,垂足分别为M、N,则![]()
∵![]() 三点在同一条直线上,
三点在同一条直线上,
![]() ∴
∴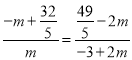 ,解得m=
,解得m=![]() .
.
3)当点A′在第三象限时,m-![]() <0,-2m+
<0,-2m+![]() <0,即
<0,即![]() <m<
<m<![]() .
.
此时点B在第四象限,显然不成立.
综上所述,m的值![]() .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
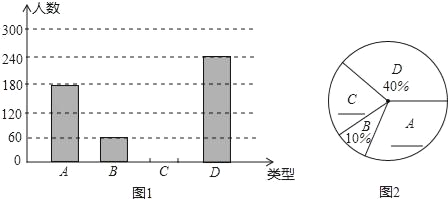
小学教材完全解读系列答案【题目】某大学举行了百科知识竞赛,为了解此次竞赛成绩的情况,随机抽取部分参赛学生的成绩,整理并制作出如下不完整的统计表和统计图,请根据图表信息解答以下问题:
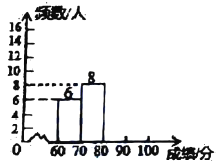

组别 | 成绩 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)表中![]() ___________.
___________.
(2)补全频数分布直方图
(3)计算扇形统计图中“![]() ”对应的圆心角度数.
”对应的圆心角度数.
(4)该大学共有![]() 人参加竞赛,若成绩在
人参加竞赛,若成绩在![]() 分以上(包括
分以上(包括![]() 分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.
分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.