Question

【题目】如图，已知△ABC，∠C = 90°，．D为BC上一点，且到A，B两点的距离相等．

（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；

（2）连结AD，若∠B = 35°，求∠CAD的度数．

Answer 1

【答案】（1）见解析；（2）∠CAD= 20°．

【解析】

(1)作AB垂直平分线，交BC于D,D就是所求点.

(2)由（1）知，AD=BD,所以可求得∠BAD，∠B与∠CAB互余，作差求得∠CAD.

解：

(1)如图所示：点D即为所求；

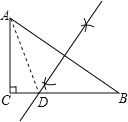
（2）在Rt△ABC中,

∵ ∠B = 35°,

∴ ∠BAC = 90° -∠B = 55°,

又∵ AD = BD,

∴ ∠BAD =∠B = 35°,

∴∠CAD =∠BAC -∠BAD = 55°- 35° = 20°．