题目内容
如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出D点的坐标______.
(2)连接线段OB、OD、BD,请直接求出△OBD的面积______.
(3)若长方形ABCD以每秒1个单位的速度向下运动,设运动的时间为t秒,问是否存在某一时刻,△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.

(1)请直接写出D点的坐标______.
(2)连接线段OB、OD、BD,请直接求出△OBD的面积______.
(3)若长方形ABCD以每秒1个单位的速度向下运动,设运动的时间为t秒,问是否存在某一时刻,△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.

(1)∵四边形ABCD是长方形,
∴AB=DC,AD=BC,
∵点A(1,8),B(1,6),C(7,6).
∴AD∥x轴,AB∥DC∥y轴,
∴D的坐标是(7,8),
故答案为:(7,8).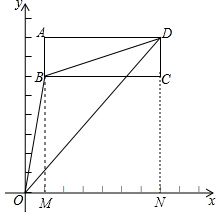
(2)延长AB交x轴于M,延长DC交x轴于N,
∵A(1,8),B(1,6),C(7,6),D(7,8),
∵OM=1,BM=6,DN=8,NM=AD=7-1=6,ON=7,
∴S△OBD=S△BMO+S梯形BMND-S△DNO
=
×OM×BM+
×(BM+DN)×MN-
×DN×ON
=
×6×1+
×(6+8)×6-
×8×7
=17.
故答案为:17.
(3)存在某一时刻,△OBD的面积与长方形ABCD的面积相等,
分为两种情况:
①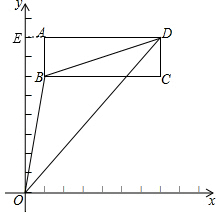
当在第一象限内时,作AE⊥y轴,S矩形ABCD=2×6=12,
则由:S△OBD=S△ODE-S△ABD-S梯形AEOB=12,
-6-
=12,
t=
;
②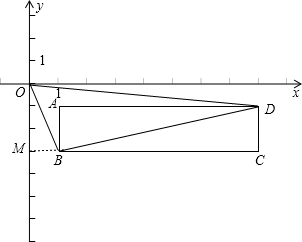
当在第四象限时,作BM⊥y轴于M,
则有:S△OBD=S梯形CDOM-S△BCD-S△BOM=12,
-6-
=12,
解得t=
∴AB=DC,AD=BC,
∵点A(1,8),B(1,6),C(7,6).
∴AD∥x轴,AB∥DC∥y轴,
∴D的坐标是(7,8),
故答案为:(7,8).

(2)延长AB交x轴于M,延长DC交x轴于N,
∵A(1,8),B(1,6),C(7,6),D(7,8),
∵OM=1,BM=6,DN=8,NM=AD=7-1=6,ON=7,
∴S△OBD=S△BMO+S梯形BMND-S△DNO
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=17.
故答案为:17.
(3)存在某一时刻,△OBD的面积与长方形ABCD的面积相等,
分为两种情况:
①

当在第一象限内时,作AE⊥y轴,S矩形ABCD=2×6=12,
则由:S△OBD=S△ODE-S△ABD-S梯形AEOB=12,
| 7(8-t) |
| 2 |
| (2+8-t)×1 |
| 2 |
t=
| 5 |
| 3 |
②

当在第四象限时,作BM⊥y轴于M,
则有:S△OBD=S梯形CDOM-S△BCD-S△BOM=12,
| 7(2+t-6) |
| 2 |
| 1×(t-6) |
| 2 |
解得t=
| 29 |
| 2 |

练习册系列答案
相关题目
 E、F.
E、F.

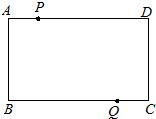 /s的速度向D移动,直到D为止,Q以2cm/s的速度向B移动.
/s的速度向D移动,直到D为止,Q以2cm/s的速度向B移动.

