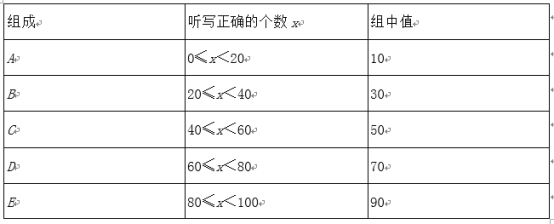
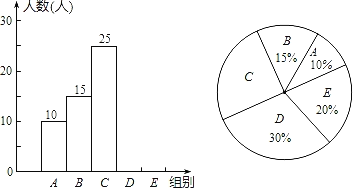
��Ŀ����
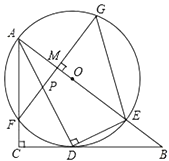
����Ŀ�� ����̼�����ɫ�������������������������ܣ�Խ��Խ�����ѡ�������г����°࣮������ij�������г��ϰ�Ӽҳ�������λ�������н��ٶ�v����/���ӣ���ʱ��t�����ӣ��仯�ĺ���ͼ�������ͼ��ʾ��ͼ���������߶�OA��AB��BC��ɣ����߶�OC����һ����T��t��0����ֱ��l��ಿ�ֵ������Ϊt�������������н���·��s���ף���
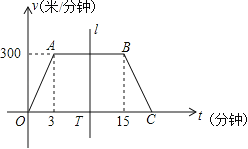
��1������t=2����ʱ���ٶ�v= ��/���ӣ�·��s= �ף�
����t=15����ʱ���ٶ�v= ��/���ӣ�·��s= �ף�
��2����0��t��3��3��t��15ʱ���ֱ����·��s���ף�����ʱ��t�����ӣ��ĺ�������ʽ��
��3��������������ϰ�Ӽҳ����н���750��ʱ���õ�ʱ��t��
���𰸡���1��![]() 200,200
200,200![]() 300��4050����2��
300��4050����2��![]() ����3��4���ӣ�
����3��4���ӣ�
��������
��1��![]() ���ݵ�A����ɵ�v=100t�����Ե�t=2ʱ��v=200,��ʱ���������ε������ʽ�����·��Ϊ200 �ף�
���ݵ�A����ɵ�v=100t�����Ե�t=2ʱ��v=200,��ʱ���������ε������ʽ�����·��Ϊ200 �ף�![]() ��t=15ʱ��v=300,��ʱ·��Ϊ
��t=15ʱ��v=300,��ʱ·��Ϊ![]() +12��300= 4050�ף�
+12��300= 4050�ף�
��2���۲캯��ͼ���֪����![]() ʱ�����������ε������ʽ�����
ʱ�����������ε������ʽ�����![]() ����
����![]() ʱ���������ε������ʽ�����
ʱ���������ε������ʽ�����![]() ��
��
��3�����������жϿɵ�t��3����ʱ![]() ����s=750���ⷽ�̼��ɣ�
����s=750���ⷽ�̼��ɣ�
�⣺��1����ֱ��OA�Ľ���ʽΪ��y=![]() t=100t��
t=100t��
��t=2����ɵã�y=200��
·��S=![]() =200��
=200��
�ʴ�Ϊ200��200��
����t=15ʱ���ٶ�Ϊ��ֵ=300��·��=![]() ��
��
�ʴ�Ϊ300��4050��
��2������0��t��3����ֱ��OA�Ľ���ʽΪ��v=kt����ͼ���֪��A��3��300����
��300=3k��
��ã�k=100��
�����ʽΪ��v=100t��
��l��OA�Ľ���ΪP����P��t��100t����
��s=![]() ��
��
����3��t��15ʱ����l��AB�Ľ���ΪQ����Q��t��300����
��S=![]() ��
��
��3������0��t��3��S���=50��9=450��
��750��50��
����3��t��15ʱ��450��S��4050��
����750=300t��450��
��ã�t=4��
������������ϰ�Ӽҳ����н���750��ʱ���õ�ʱ��4���ӣ�

 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�